综合评价法及其基本步骤：确定环境要素权重系数

运用多个指标对多个参评单位进行评价的方法，称为多变量综合评价法，简称综合评价法。其基本思想是将多个指标转化为一个能够反映综合情况的指标来评价。如不同国家经济实力、不同地区社会发展水平等，都可以应用这种方法。

综合评价法的基本步骤包括以下方面：

3.2.2.1 确定环境要素权重系数

权重系数一般采取层次分析法进行综合确定。其基本分析步骤为：

1.建立层次结构模型

按投资环境因素的内容及相互关系，将各环境要素划分为层次结构形式，即对投资环境因素及其所包含的子因素由上到下逐层进行分析，根据因素和指标确定原则来确定每一层所包含的因素，建立起一个有序的递阶层次结构，最后一层为具体的评价指标层。

2.确定同层间简单权重系数

同层间要素的简单权重系数是用以描述位于同一层次的各环境要素相对于上一层因素重要程度的系数。它是由求解该层的判断矩阵求得的。判断矩阵则是由同一层次间各要素之重要程度两两比较而构建的。为了便于清晰地界定因素的重要程度，将评价尺度按表3-2划分为9＜1～1＜1，共9个级别。其中9＜1表示绝强的相对重要程度，1＜1表示等强的相对重要程度。其由极强而强，由强而稍强、等强，逐次变化。绝弱到等弱，则与绝强到等强的含义相反。

表3-2 相对重要程度评价尺度表

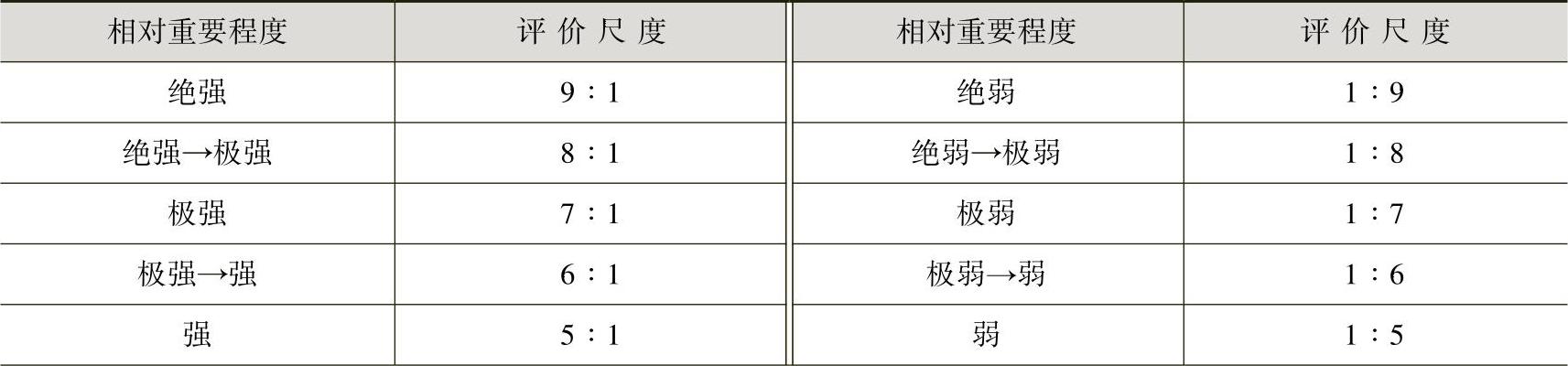
（续）

由此，一个由几个要素构成的同一层次结构，经因素间相对重要性判断之后，便可构造一个n×n阶的矩阵，即判断矩阵。构造好判断矩阵后，运用线性代数方法，计算判断矩阵的特征向量，便可求得同层间简单权重系数。

3.一致性检验

如前所述，判断矩阵是由分析者在对各因素的相对重要程度进行两两比较后，凭估计而建立起来的。既然是估计，就难免存在误差，而过大的误差会影响简单权重系数的可信度。因此，需要一种检验及度量这种判断误差大小的方法，即一致性检验法。

一致性检验的公式为：

式中，CI为一致性检验指标；λ_max为判断矩阵最大特征值；n为判断矩阵的阶。

由于λ_max≥n，故CI一般均大于或等于零。当CI太大时，就认为该判断矩阵的一致性太差，所求得的简单权重系数不可信，需要重新进行相对重要性的判断。一般来说，只要CI值小于0.1，便认为这个判断是令人满意的。

4.组合权重系数的确定

在上述各层的权重系数确定以后，便可由递推运算判定各层间因素的组合权重系数。组合权重系数描述的是综合考虑了上下两层各因素的权重系数后，得出的相对于更上一层相应因素的权重系数，即优先函数。

设某项目投资环境层数为A、B、C三层，由判断矩阵已求得B层、C层各因素的简单权重系数分别为b_i和c_ij，则C层各因素的组合权重系数为BC_j，可按下式计算：(www.xing528.com)

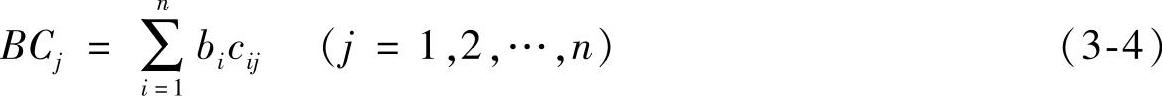
组合权重系数BC_j描述了C层各因素相对于A层的优先顺序。若C层下还有一层因素D，其简单权重系数为d_ij，则该层相对于A层的优先顺序BCD_j，按下式递推运算求出：

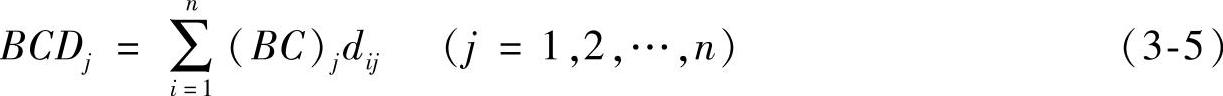
由上而下，以此递推，便可求得层次结构模型的最下层投资环境因素在环境分析中的组合权重系数。

3.2.2.2 各投资环境要素的评分

组合权重系数仅仅描述了各环境要素在投资环境分析中的重要程度。对要素的单项评价，还须通过计分的方法来实现。通常的做法是，不论其为定性还是定量指标，均按优、良、中、差四级进行评价。为了评价结果更符合客观实际，应综合考虑全部评价者对j指标的评价，可按下式计算：

V_j=4r_j1+3r_j2+2r_j3+r_j4 （3-6）

式中，V_j为投资环境指标j的评分值；r_j1为j指标为优的评价者占全部评价者的百分比；r_j2为j指标为良的评价者占全部评价者的百分比；r_j3为j指标为中的评价者占全部评价者的百分比；r_j4为j指标为差的评价者占全部评价者的百分比。

3.2.2.3 投资环境的综合评分

分别求出各环境要素的组合权重系数BCD_j和评分值V_j后，便可代入下式求目标投资环境的综合评分：

式中，G为目标项目投资环境综合评分；BCD_j为第j个环境要素的权重系数；V_j为第j个环境要素的评分值；n为环境要素的个数。

上式求得的分值在1～4分之间，分值越高，说明目标项目投资环境评价越好。

3.2.2.4 投资环境的敏感性分析

前述投资环境的综合评价，是一种静态评价。现实社会经济生活是动态的过程，敏感性分析正是要考察环境条件变化时，将对分析结果带来的影响及其程度。其步骤如下：

（1）逐项分析环境因素的稳定性，判断其在房地产投资建设或经营期内发生变化的可能性，并研究其变化的基本趋势及变化程度。

（2）对将要发生变化的因素，依据其变化的趋势及变化程度，请专家给予重新评价。

（3）统计各因素的评价结果，计算它们的分值。

（4）计算变化后的住宅市场投资环境综合评分值。

（5）若是不同地点投资环境的比较和排序，则按新的综合评分值重新排序，并比较前后两种排序的差异，分析原因，作出判断。

（6）若是单一项目、单一地点的投资环境分析评价，则比较前后两次综合评分值，研究其变化程度，分析原因，作出判断。