资金等值的计算方法优化方案：

2.2.2.1 资金等值相关概念

发生在不同时点上的两笔或一系列绝对数额不等的资金额，按资金时间价值尺度，所计算出来的价值相等，称为资金等值（Equivalence）。等值可以是一对一的，也可以是一个现金流对应发生在不同时点上的一系列现金流，以及一系列现金流对应一个现金流的等值。资金等值的概念包括三个因素：现金流量（资金）的大小、利率及现金流量（资金）发生的时点。资金在某一时点上等值，则它在任意其他时点上也等值。

通常情况下，在资金等值计算中，人们把资金运动起点时的金额称为现值（P），把资金运动结束时与现值等值的金额称为终值或未来值（F），把资金运动过程中某一时间点上与现值等值的金额称为时值，把某一时间序列各时刻发生的资金称为年值（年值相等时称为等额年值A，否则称为不等额年值）。时值是点值，年值是序列值。另外，把未来时点发生的资金用资金时间价值的尺度（如利率i）折算成现在时点相应资金数额的过程，称为折现（或贴现）。把某一时间序列其他各时点的资金折现到资金运动起点的资金值，也称为现值（P）。本金就是一种现值。把某一时间序列其他各时点的资金折算到资金运动终点的资金值，也称为终值（F）。本利和就是一种终值。

2.2.2.2 资金等值的计算

资金等值的计算通常主要涉及三项内容：求终值、求现值及求等额年值。

1.终值的计算

（1）已知现值P、利率i、计息周期n，求终值F。此问题也是复利终值问题，其计算公式见式（2-4），式中的（1+i）n称为“复利终值系数”，记作（F/P，i，n）。

（2）已知等额年值A、利率i、计息周期n，求终值F。此问题也是年金终值问题，其

计算公式为：

式中的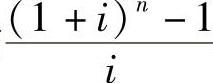称为年金终值系数，记作（F/A，i，n）。

[例2-1] 某投资项目，5年中每年年末向银行贷款50万元，年利率为8%，第5年年末一次还本付息，则应偿还的本息和是多少？

解：

已知A=50万元，i=8%，n=5年

根据式（2-7），可以求得第5年年末应偿还的本息和为：

F=50万元×[（1+8%）5-1]/8%=293.33万元

2.现值的计算

（1）已知终值F，利率i，计息周期n，求现值P。此问题就是复利现值问题（折现问题）。其计算公式为：

式中的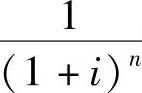称为复利现值系数，记作（P/F，i，n）。

（2）已知等额年值A，利率i，计息周期n，求现值P。此问题称为年金现值问题。其计算公式为：

式中的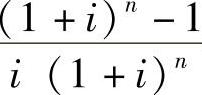称为年金现值系数，记作（P/A，i，n）。

[例2-2] 某家庭预计今后10年内的月收入为16000元，如果其中的30%可用于支付住房抵押贷款的月还款额，年贷款利率为12%，问该家庭有偿还能力的最大抵押贷款申请额是多少？

解：

已知该家庭每月可用于支付抵押贷款的月还款额A=16000元×30%=4800元(www.xing528.com)

月贷款利率为i=12%/12=1%，计息周期为n=10×12=120

根据式（2-9），可以求得该家庭有偿还能力的最大抵押贷款额为：

P=4800元×[（1+1%）120-1]/[1%×（1+1%）120]=334562.51元

3.等额年值的计算

（1）已知终值F，利率i，计息周期n，求等额年值A。此问题称为资金存储问题，是指为了在若干年后偿还一笔债务或积累一笔投资，每年必须存储的资金。其计算公式为：

式中的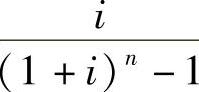称为资金存储系数，记作（A/F，i，n）。

[例2-3] 某购房人想在5年后一次性付款，购买一套面积为50m²、单价为5000元/m²的房屋用于投资。假设银行存款利率保持3%不变，问从现在开始的每一个月月末他应存多少钱才能在5年后实现自己的买房投资愿望？

解：

已知F=50m²×5000元/m²=250000元，月利率i=3%/12=0.25%，n=5×12=60

根据式（2-10），可以得到月存款额为：

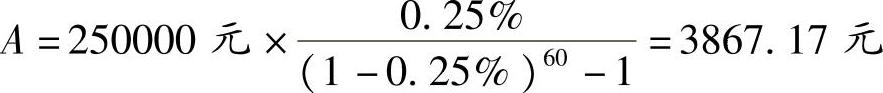
（2）已知现值P，利率i，计息周期n，求等额年值A。此问题称为资金回收问题，即一定期限内，分期偿还一笔利率固定的债务或收回一笔利率固定的投资。其计算公式为：

式中的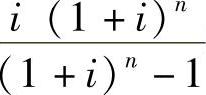称为资金回收系数，记作（A/P，i，n）。

[例2-4] 某家庭以抵押贷款的方式购买了一套价值为25万元的住宅，如果该家庭首付款为总房款的30%，其余房款用抵押贷款支付，抵押贷款的期限为10年，按月等额偿还，年贷款利率为15%，问月还款额为多少？

解：

已知抵押贷款额P=25万元×70%=17.5万元

月贷款利率i=15%/12=1.25%，计息周期n=10×12=120

根据式（2-11），可以求得月还款额为：

A=175000元×[1.25%×（1+1.25%）120]/[（1+1.25%）120-1]=2823.4元

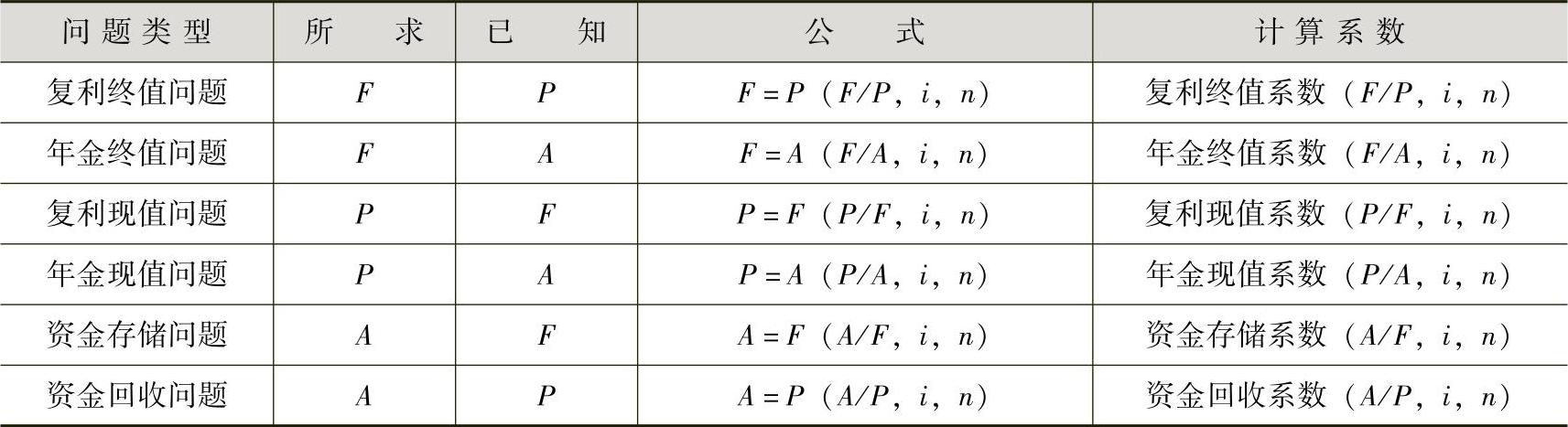
以上六类基本等值问题的计算公式可以汇总在表2-2中。

表2-2 资金等值计算基本公式