【摘要】:我们将6.2.2小节的多项式时间动态规划算法采用MATLAB编程实现,并应用到一个算例中,以验证该算法的适用性。表6-1算例参数续表根据表6-1中问题的参数,用本章动态规划算法求得的最优成本为352,对应变量的最优结果如表6-2所示。图6-4算例结果网络流图示图6-4直观地显示了算例的最优解结果。在第1期,网络零售商采用自营物流从订单处理中心发送21单位货品到配送站,满足该期13单位的需求,剩下8单位货品作为期末库存来满足第2期需求。
我们将6.2.2小节的多项式时间动态规划算法采用MATLAB编程实现,并应用到一个算例中,以验证该算法的适用性。算例的基本参数如表6-1所示。
表6-1 算例参数
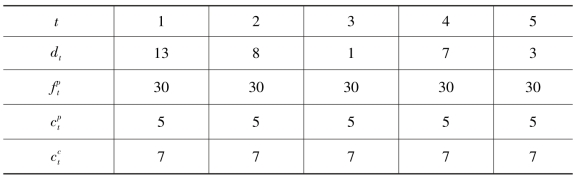
续表

根据表6-1中问题的参数,用本章动态规划算法求得的最优成本为352,对应变量的最优结果如表6-2所示。
表6-2 算例最优结果(https://www.xing528.com)

注:最优成本为352。
将表6-2中算例的最优结果用网络流表示,如图6-4所示。

图6-4 算例结果网络流图示
图6-4直观地显示了算例的最优解结果。在第1期,网络零售商采用自营物流从订单处理中心发送21单位货品到配送站,满足该期13单位的需求,剩下8单位货品作为期末库存来满足第2期需求。第3期到第5期则分别采用第三方物流从订单处理中心发送到配送站,然后立即从配送站来满足当期需求。
另外,我们也采用了智能优化软件CPLEX中的混合整数规划模块对6.1.2小节的模型进行了求解。结果和表6-2一致,这也进一步验证了本研究动态规划算法的有效性。不过,对于企业来说,智能优化软件的购置成本较高,而本章设计的算法则能用任何编程语言轻松实现,且在求解问题的效率更高,从而有效降低企业运营成本,提高决策水平。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




