在6.1.3小节网络流模型的基础上,对问题的最优解进行性质分析,以期能够在这些性质的基础上设计多项式时间内的动态规划求解算法。首先,根据文献[130],有如下定义:
定义6.1 假设(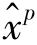 ,
,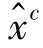 ,
,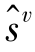 ,
,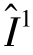 ,
,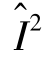 )为一条可行流,即对应着问题的一个可行解。如果不存在另外两条可行流(
)为一条可行流,即对应着问题的一个可行解。如果不存在另外两条可行流(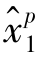 ,
,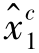 ,
,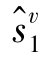 ,
,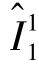 ,
,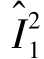 )和(
)和(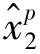 ,
,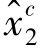 ,
,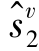 ,
,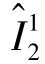 ,
,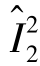 )使得(
)使得(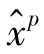 ,
,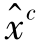 ,
,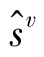 ,
, ,
,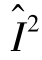 )=(
)=(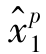 ,
,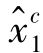 ,
,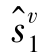 ,
,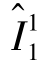 ,
, )+(
)+(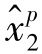 ,
,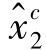 ,
,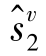 ,
,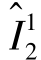 ,
,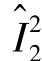 ),则(
),则(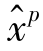 ,
,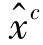 ,
,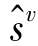 ,
,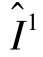 ,
,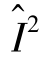 )是一条极流。
)是一条极流。
在问题的可行区域内,如果能够求得目标函数的有限全局最小值,则一定有一个极流是最优流,即最优解。由于可行区域内只有有限数目的极流,因此,可以通过搜索所有可能的极流来得到最优流。不过,这样遍历的效率非常低,而分析该问题极流的性质则能简化这个搜索过程。接下来,就重点分析本章研究问题的相关性质。
引理6.1 在凹性成本结构的单一起点网络流模型中,极流的任意一个节点至多有一个正的输入流[2]。
本章研究的问题可以由一个单一起点的网络流模型表示(图6-2),且每条弧对应的成本结构都是凹性的,所以由引理6.1可知,在问题的最优解中,即该网络流的最优流中,任意节点至多只会有一个正的流入,也就是说,任意一个节点至多只能从其他一个节点接受货品。
引理6.2 在最优解中,对任意时期t=1,2,…,T,当且仅当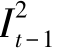 <dt时,
<dt时,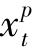 +
+ >0。
>0。
证明 (1)当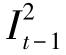 <dt时,有
<dt时,有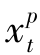 +
+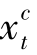 >0。因为缺货不被允许,因此,在最优解中,当
>0。因为缺货不被允许,因此,在最优解中,当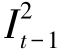 <dt时,dt不能被上一期末配送站处库存
<dt时,dt不能被上一期末配送站处库存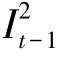 全部满足,则必有
全部满足,则必有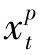 +
+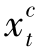 >0。
>0。
(2)当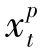 +
+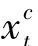 >0时,也有
>0时,也有 <dt。假设在最优解中,
<dt。假设在最优解中,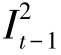 ≥dt且
≥dt且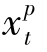 +
+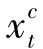 >0,由于订单处理中心处单位库存持有成本小于配送站处单位库存持有成本(h1<h2),于是将t期的配送量
>0,由于订单处理中心处单位库存持有成本小于配送站处单位库存持有成本(h1<h2),于是将t期的配送量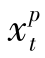 +
+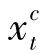 减少到零,将其推迟到t期之后配送能得到一个新的可行方案,并使得成本比原来方案要小(
减少到零,将其推迟到t期之后配送能得到一个新的可行方案,并使得成本比原来方案要小(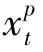 +
+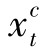 )·(h2-h1),这与初始假设为最优解矛盾。(https://www.xing528.com)
)·(h2-h1),这与初始假设为最优解矛盾。(https://www.xing528.com)
证毕。
性质6.1 在最优解中,对任意时期t=1,2,…,T,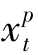 ·
·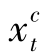 =0。
=0。
证明:假设在最优解中,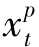 ·
· >0,即
>0,即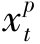 >0且
>0且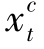 >0。于是,相应的发货成本为
>0。于是,相应的发货成本为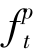 +
+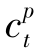 ·
·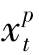 +
+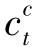 ·
·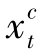 。当
。当 ≤
≤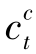 时,减少
时,减少 为零并将
为零并将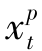 增加为
增加为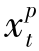 +
+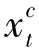 ,得到一个新的可行解,总成本为
,得到一个新的可行解,总成本为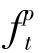 +
+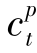 (
(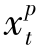 +
+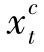 ),且小于原来的成本;当
),且小于原来的成本;当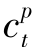 >
>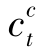 时,减少
时,减少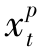 为零并将
为零并将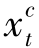 增加为
增加为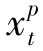 +
+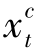 ,也可得到一个新的可行解,总成本为
,也可得到一个新的可行解,总成本为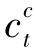 (
(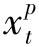 +
+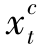 ),也小于原来的成本,这都与原假设为最优解矛盾。
),也小于原来的成本,这都与原假设为最优解矛盾。
证毕。
性质6.1表明,在最优解中,若任意时期需要从订单处理中心运送货品到配送站,则只会采用一种模式运输,要么采用自营物流配送,要么采用第三方物流配送。
性质6.2 在最优解中,对任意时期t=1,2,…,T,(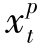 +
+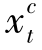 )·
)·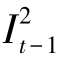 =0。
=0。
证明 首先由引理6.2,在最优解中,只有当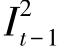 <dt时,
<dt时,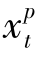 +
+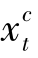 >0。进一步的,由性质6.1可知,最优解中若某时期t有货品从订单处理中心运送到配送站,则该时期
>0。进一步的,由性质6.1可知,最优解中若某时期t有货品从订单处理中心运送到配送站,则该时期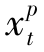 和
和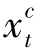 有一个为零,另一个则等于该运送量,即在最优流中,弧(t,t′)上承载着正的流进入到配送站节点t′。而引理6.1表明,在最优流中,一个节点最多只有一个正的流入,所以流入配送站节点t′的库存
有一个为零,另一个则等于该运送量,即在最优流中,弧(t,t′)上承载着正的流进入到配送站节点t′。而引理6.1表明,在最优流中,一个节点最多只有一个正的流入,所以流入配送站节点t′的库存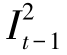 必为零。同样由引理6.1,若最优流中,流入配送站节点t′的库存
必为零。同样由引理6.1,若最优流中,流入配送站节点t′的库存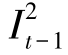 为正,则弧(t,t′)上承载的流都为零。
为正,则弧(t,t′)上承载的流都为零。
证毕。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




