单一顾客类型情境下的案例分析

1.基本应用

公司J是国内一家领先的生鲜电商，顾客在其网上商店下单后，该电商会把货物配送到离顾客最近的保鲜自提柜以完成交付。笔者在调查该公司时了解到，生鲜产品的需求呈现动态变化的特征，通常表现为：工作日需求量大，周末需求量小。这是因为大多数顾客在工作日没有时间去市场采购，从而选择网上购买，到周末则多半会选择自己到线下市场购买。面对如此动态变化的需求，以及生鲜产品的短保质期特征，公司J需要频繁地向其订单履行中心附近的一家大型农产品交易中心采购，供应提前期大约只有一个半小时，保证了充足且及时的供应。

本节为研究单一顾客类型的纯网络零售情境下的补货计划问题，选取了该电商的星级产品“营养套餐”。这种自制的套餐由不同种类的新鲜蔬菜和肉类组成，商家买来各种食材后按比例快速搭配制作就相当于该产品的补货过程。经过实地访问，我们得到了该产品自2013年8月26日至9月4日（T＝10天）的成本参数。其中，固定订购成本（st），包括原材料运输成本、人工成本和能源成本，为20元。每份套餐中所有配料的单位购买成本（pt）为21.5元。尽管pt在不同时期t可能会变化，但访问的这10天内波动很小，所以假设其恒定为常数。单位库存持有成本（ht＝7元）相对较高，因为该营养套餐的保质期很短，仅为3天。补货后每多持有一天，就会提高变质风险。当顾客订单在应交付日期之后才被满足，每一延迟的时期，都会产生一单位的延迟惩罚成本（bt＝1元），主要是给顾客的小补偿。在如此短的计划周期内，不考虑折现因素。此外，该营养套餐的单位售价为28元，所有顾客的需求提前期都是两天（L＝2），允许的最大延迟交付时间是一天（G＝1）。表4-1为单一顾客类型的纯网络零售情境下“营养套餐”的实验结果。

表4-1　单一类型顾客情境下“营养套餐”的实验结果

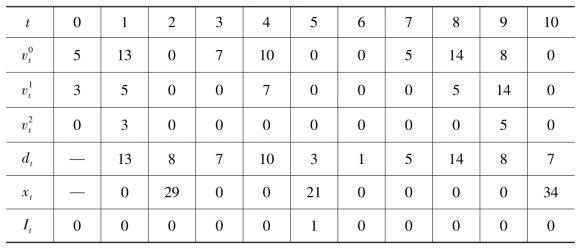
注：十天规划期的最优成本为1881元。

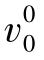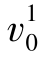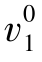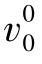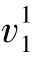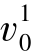由表4-1的结果可知，在第1天初（即第0天末），系统有两类提前需求：一类为一天之前到达的5个订单（），另一类为两天之前到达的三个订单（）。第1天没有生产性补货，所以当日抵达的13个订单（d1）转移成第2天初（第1天末）的提前需求订单，且转移为，转移为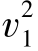。第2天生产补充的29份套餐正好满足所有的提前需求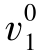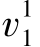（、和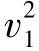）和当日抵达的需求（d2）。在最优解中，只有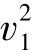和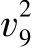招致了延迟惩罚成本，而其他提前需求则没有。最终得到的最优补货计划为：在第2天生产补充29份，第5天生产补充21份，第10天生产补充34份。

当该电商不使用提前需求信息，即当L＝0，G＝0时，采用基本的动态批量补货计划的总成本为1993元，而采用本研究考虑提前需求信息（L＝2，G＝1）的方法后，总的成本为1881元，比原先降低了5.6%。

2.L和G的价值

接下来，本小节依然采用公司J的数据进行数值实验，探究L和G的不同取值如何影响最优总成本。由于单位购买成本pt并不影响最终决策，可以技术上将其设为0（pt＝0）。另外，为了便于实验的实施，假设规划期初的提前需求也为0（即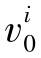＝0）。图4-1显示的是当L和G的取值从0到4变化时对应的最优成本变化情况。(www.xing528.com)

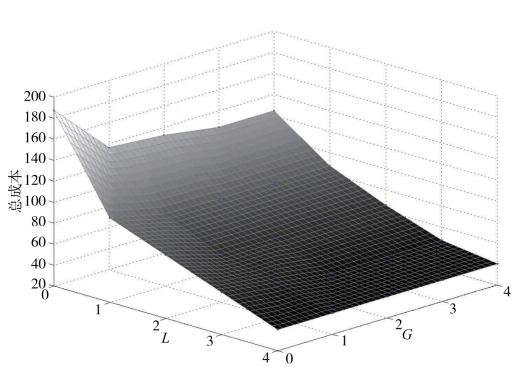
图4-1　单一顾客类型情境下不同L和G对应的最优成本

当L＝G＝0时，问题就变成一个经典的Wagner-Whitin问题，其中，t时期到达的需求必须在当期立即得到满足。从图4-1可以看到，这种情况下的总成本要比L（或G）大于零时大得多。该结论意味着决策者可以利用需求提前期或者允许的延迟交付时期来减少总的库存成本。这也和实际中一些网络零售商为了鼓励顾客等待而提供免费配送服务的做法相符。当G＝0（即延迟配送不被允许）时，最优总成本随着L的增加而减少。从中可以发现一条管理启示，即L值越大，就能带来更多的需求信息，于是商家也就可以利用这些提前需求信息来节省更多的成本。其中还蕴含着另一条管理启示，即L值越大，零售商在规划期内满足需求的弹性就越大，就不必由于延迟配送而招致惩罚成本。经营者可以平衡获取提前需求信息的成本和它所能节省的成本，进而决定合适的L。从图4-1还可以发现，当L＝0时，总的最优成本随G也递减，但是节约成本的效果没有L显著。通过进一步观察当L＝4时总成本的变化情况，可以发现G的变化基本对降低成本没有作用。然而，当G＝4时，L的增加依然对成本降低有显著作用。

3.bt与ht比值的影响

进一步，我们设计一个数值实验来观察单位库存持有成本bt与单位延迟惩罚成本ht的比值对最优成本的影响。假设bt与ht的值恒定，即与t无关。除了bt和ht，依然采用公司J的数据来进行实验。

ht和bt的绝对大小对最优总成本的影响很大，为了减少这种作用，以便能够更好地分析bt与ht不同的比值对最优成本的影响，设计在bt+ht的值被固定的情况下再来变化bt与ht的比值。实验分别在bt+ht被固定为2、4和6三种情况下进行，结果如图4-2所示。

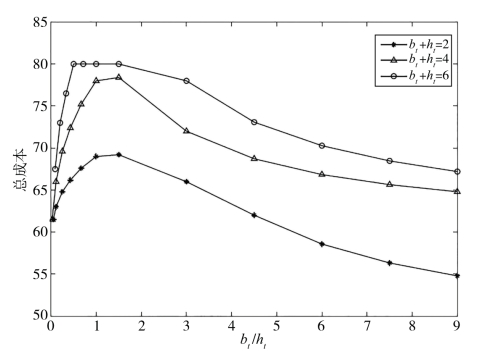
图4-2　不同的bt与ht比值对应的最优成本

图4-2显示，当bt+ht分别等于2、4和6时，bt与ht比值的变化对最优成本的影响呈现出一致性的特征。最优成本随着bt与ht的比值的增加先迅速增加，再逐渐缓慢变小。特别地，当bt与ht的比值从零开始增长时，最优成本增加最快，并在bt与ht的比值达到1附近时，最优成本达到最大值。当bt与ht的比值大于1时，最优成本下降缓慢。另外，从图中也可以看到，在bt+ht取值较大时，平均的最优成本也较大。