多项式求解算法的分析介绍

由上节的两个最优性质可知，对任意需求类别k，都有唯一的满足期γ（k）。而且，γ（k）要么是一个补货期，要么γ（k）＝Ak。

根据先到先被服务（FCFS）的规则，不同类别的需求是根据其下标序号的顺序来被满足的。也就是说，对任意k（2≤k≤N），γ（k）≥γ（k-1）。

进一步，可以得到以下性质：

性质4.3　在最优解中，任意两个相邻的补货期t1与t2之间存在这样一个需求类别n，使得t1≤γ（n）＜t2，且Iγ（n）＝0。

证明　采用反证法。假设在某一含有两个相邻补货期t1和t2的最优解中，要么没有这样一类需求n满足t1≤γ（n）＜t2，要么当任意n满足t1≤γ（n）＜t2时，Iγ（n）＞0。

首先考虑不存在需求类别n使得t1≤γ（n）＜t2的情况。由性质4.1和性质4.2可知，在这种情况下，对任意1≤k≤N，以及任意t1≤t＜t2，都有rk，t＝0。将这些补货时期内的补给量全部安排到单一补货期是可行的，且会得到一个新解，使得总成本不超过初始解对应的成本。这就意味着，要么初始解不是最优的（与假设相矛盾），要么新的可行解也是最优解。

然后，考虑当任意n满足t1≤γ（n）＜t2时，Iγ（n）＞0的情况。让n*表示满足该条件的所有n中的最大值。由性质4.1和4.2，在此情况下，对任意n*＜k≤N，以及任意γ（n*）≤t＜t2，都有rk，t＝0。若，将时期t1补货中数量等于的部分转移到时期t2，这样会得到一个未增加成本的新可行解。而且，在新解中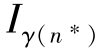＝0。

若，将t2时期所有的补货量转移到t1时期会得到一个严格优于初始解的新可行解，这也和初始解为最优解的原假设相矛盾。

证毕。

接下来，定义满足Iγ（n）＝0和γ（n+1）＞γ（n）这两个条件的需求类别n为奇异需求类。例如，假设某一需求类别k，其中Ak＝2，Bk＝4，Ck＝5，有单一的满足期γ（k）＝3，同时该满足期也必然是补货期。如果I（3）＝0，且需求类别k+1的满足期为γ（k+1）＝5，时期3的补货量就只能满足到需求类别k，而不能满足需求类别k+1。因此，需求类别k就是一个奇异需求类。根据定义，需求类别N也是一个奇异需求类。根据以上的性质，可以得到如下推论：

推论4.1　对任意两个相邻的奇异需求类n1和n2，存在唯一的补货期τ，使得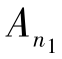≤γ（n1）＜τ≤γ（n2）。

证明　显而易见，γ（n1）和γ（n2）之间至少存在一个补货期，因为需求类n1，n1+1，…，n2需要在这些期被满足，而且＝＝0。

如果γ（n1）和γ（n2）之间存在不止一个补货期，则这些补货期之间不存在奇异需求类就和性质4.3相矛盾。

证毕。

定义F（n）为满足需求类别1，2，…，n的总成本，且n是一个奇异需求类。于是，可以得到如下递归方程：(www.xing528.com)

其中，f（k，t，n）表示已知k和n两类需求为奇异类需求时，在时期t补货来满足需求类别k+1，…，n的总成本。

由式（4.14）和式（4.15）可知，只要知道f（k，t，n），就可以采用动态规划方法解决问题。其中，式（4.14）为初始条件，式（4.15）为递归方程。

如果定义

式（4.15）就可以被重新写成

根据定义，f（k，t，n）就可以被重新写为

其中，

很明显，所有的αl，t、βl，t和Gl，t都可以在O（NT）时间内计算得到。

因此，式（4.15）可以重写为

其中，

初始条件为：

于是，以式（4.14）和式（4.19）为初始条件，由式（4.17）和式（4.18）分别递归计算F（n）和Q（n，t），就可以解决问题。具体的计算过程为：

F(0)，Q(0，t)，t＝1，2，…，T→Q(1，t)，t＝1，2，…，T→F(1)→Q(2，t)，t＝1，2，…，T→…→Q(N，t)，t＝1，2，…，T→F(N)。

最优解对应着F（N），且可由前向后递归计算得到。该方法总的计算复杂度为O（NT）。