统一模型下需求时间窗的最优性质分析

本节对上节中考虑需求时间窗的统一模型进行分析，得到如下几条最优解性质：

性质4.1　在最优解中，对任意k＝1，2，…，N，和任意t∈[Ak，Ck]，如果rk，t＞0，则要么t＝Ak，要么xt＞0。

证明　假设在最优解中，对某一需求类别k和某一时期t，有k＝1，2，…，N，t＞Ak，rk，t＞0，且xt＝0。那么必然有一时期τ（0＜τ＜t），且xτ＞0，定义τ*为满足条件的τ的最大值。

让t′＝max（τ*，Ak）＜t，构建一个和初始最优解相同的解，除了r′k，t′＝rk，t，以及r′k，t＝0（满足k类需求的时期由t转移到t′）。该新解是可行解，对应的t′到t-1期的库存持有水平减少，且延迟交付的水平也降低了。也就是说，新解对应的总成本比初始最优解还要低。这就和最初假设初始解为最优解相矛盾。

证毕。

性质4.2　在满足性质4.1的最优解中，对任意k＝1，2，…，N，只有一个时期t，使得t∈[Ak，Ck]，且rk，t＞0。(www.xing528.com)

证明　同性质4.1一样，采用反证法证明。假设在一个最优解中，存在某一需求类别k，以及时期t1和t2，使得Ak≤t1≤t2≤Ck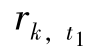，＞0，且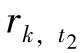＞0。根据假设以及性质4.1，t2＞Ak就意味着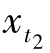＞0。

定义τ为满足τ≤t1的最近补货时期。根据模型约束，这样的时期τ一定存在。

如果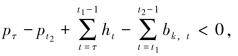让Δ＝min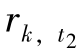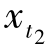（，），并按以下方式构建一个新解：将时期t2的补给量Δ移到时期τ，同时将时期t2的需求满足量Δ转移到时期t1。于是，订购成本会增长（pτ-pt2）Δ。时段τ到t1-1内的每一期会增加Δ的持有库存，时段t1到t2-1内的每一期都会减少相同数量的延迟交付量。由此，得到的新解要严格优于初始最优解，这和假设相矛盾。

同样的，如果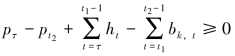时，也可以像以上证明过程一样构建一个严格优于初始假设最优解的新解，使得原假设不成立；或者构建的新解与初始解有相同的成本，不过对需求类别k来说，新解中要少一满足时期，意味着新解也是最优解。

证毕。