连续时间批量研究方案优化

在1.2.2节介绍的离散型动态批量模型中，时间被假设成是离散的，且需求也随时间动态变化。而另一大类批量问题则考虑连续的需求率，即时间是连续不间断的。解决这类问题的模型被称为连续型经济批量模型，因为其通常是在经济订货批量（EOQ）模型的基础上发展而来的。在连续时间批量问题中，决策变量一般为固定的订货周期和订货量。另外，文献中关于此类问题的研究又主要分为单产品的EOQ问题和多产品的联合补货问题（joint replenishment problem，JRP）。

1.单产品EOQ模型

EOQ模型是运作管理中最基本的库存模型之一，最早由Harris（1913）提出。基本的EOQ模型假设在无限计划周期内有着稳定且连续的需求率，即需求以恒定速率不断地发生。决策者需要通过频繁订货来满足需求，且每次订货会产生固定订购成本，订货后未消耗完的产品要作为库存并导致持有成本。因此，EOQ问题的核心优化问题在于订购成本与持有成本之间的平衡。若假设需求率为D（单位时间需求数量），每次订购的固定成本为K，单位产品在单位时间的库存持有成本为h，订货量为Q，以及订货周期为T，基本EOQ模型中库存水平与时间的关系可由图1-3表示。

图1-3　基本EOQ模型

由图1-3可知，在订货量为Q的情况下，固定订货周期为平均每单位时间内的订购成本就为。另外，库存水平在每次补货后立即上升到Q，然后以需求率D的速度消耗至零库存点，随即发生的下一次订货又将其提高至Q。像这样，库存水平以周期T循环变化。因此，整体的平均库存水平就为，即平均每单位时间内都对应持有这么多库存，对应的持有成本就为。于是，单位时间内的平均总成本就等于。通过对平均总成本求关于Q的一阶导数，可以找到最优订货量为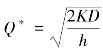，并进一步求得最优订货周期为以及最优总成本为。在EOQ模型的最优解中，即平均订货成本等于平均持有成本。(www.xing528.com)

基本EOQ模型解决的是最简单的单产品连续时间批量补货问题，已有文献中有许多拓展研究。本书在这些EOQ模型理论的基础上，为网络预售新产品的的补货问题分别构建了预售期不固定情形下的一次补货模型和预售期固定情形下的两次补货模型。网络预售新产品的特点在于其销售期短，且商家在预售期内缺货完全拖后。基于这些特点，本书引入了BASS扩散模型来构造连续需求函数，且提出了已有文献中尚未研究的起始有缺货的两次订货模型。在第5章中，本书将详细讨论与此问题相关的研究。

2.多产品JRP问题

JRP问题最早由Andres和Emmons（1976）提出，它考虑同时为多个产品制订订购计划，利用经济规模效应来降低补货成本，是EOQ的一般化问题。然而，与EOQ模型不同的是，JRP问题中某一产品在其每个补货点的订购量不一定相等。不过，许多学者在研究此类问题时，却会为每种产品设置相同订货周期和订货量的方案（Goya和Satir，1989）。若假设有n个产品，每一产品i（i＝1，2，…，n）都有稳定且连续的需求率Di，对应的固定订购成本为Ki，单位时间内的库存持有成本为hi，而且只要有产品订购就会触发联合固定订购成本K0，基本的JRP问题可由如下模型表示：

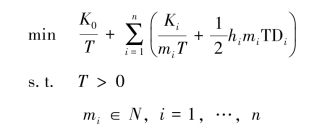
其中，决策变量T是基础的补货周期，miT（mi∈N）为产品i的补货周期。也就是说，产品i每隔mi个T时间，会被订购一次。

在基本JRP问题中，只要两个决策变量T和mi中的一个已知，就很容易求得另一个的最优值。但实际问题却是要同时求得这两个决策变量的最优值，Arkin等（1989）通过3-SAT问题多项式时间内归约的方法，证明了JRP问题为强NP难题。文献中有许多关于JRP问题的模型与解决方法研究，具体可见参考文献[91][93]。