离散时间动态批量研究：优化标题的策略

动态批量（dynamic lot-sizing，DLS）模型是库存管理领域的经典模型，它考虑的是动态离散需求环境下的生产计划或库存补给问题，最初由Wagner和Whitin（1958）与Manne（1958）提出。DLS问题曾被评为管理科学领域十个最具影响力的问题之一。在近半个多世纪里，学者们围绕这一问题在不同方向上进行了诸多拓展研究，相关的研究综述也非常多。例如，De Bodt等（1984）对基本的DLS问题和相应的解决技术进行了详细的分析与探讨，并强调了DLS在实际生产环境中的应用，尤其是面临动态需求的MRP领域；Bahl等（1987）从能力约束和问题的层级这两个维度将DLS问题划分为四类：单层级无能力约束问题、多层级无能力约束问题、单层级有能力约束问题，以及多层级有能力约束问题；Karimi等（2003）对有能力约束的DLS问题从模型和算法上进行了综述；Brahimi等（2006）重点讨论了文献中对单产品DLS问题的研究，总结了无能力约束问题和有能力约束问题不同的建模手段和解决方法；Jans和Degraeve（2007）则专门讨论了文献中解决有能力约束DLS问题的元启发式算法（meta-heuristics）。

Wagner和Whitin（1958）最初提出的是一个单物品无能力约束的DLS问题，并采用混合整数规划构建了标准模型，具体如下：

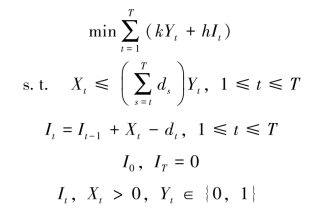
其中，T为问题的总规划期数，k为生产或补给的固定启动成本，h为单位产品单期的库存持有成本，dt（t＝1，…，T）为时期t的确定性需求。问题的决策变量为Xt（时期t的生产或库存补给量），Yt（时期t是否启动生产或补给的0-1决策变量），和It（第t期末的库存持有量）。基本的决策问题就是，在规划期内哪些期启动生产或补给，对应的补给量是多少。解决基本DLS问题的核心是零库存点订购（zero inventory ordering）性质，即在任意时期t，都有It-1·Xt＝0。也就是说，在规划期的任意时期，要么由上一期末的库存来全部满足该期需求，要么在该期实施补给来满足自当期向后整数期的所有需求。根据该最优性质，Wagner和Whitin（1958）设计了复杂度为O（T2）的精确动态求解算法。

针对DLS基本问题，后续学者首先从模型构建上进行了诸多研究，包括采用网络流模型、设施选址规划模型等对原问题进行重新建模。其中，最有影响力的为网络流方法（Zangwill，1969），其具体模型如图1-2所示。

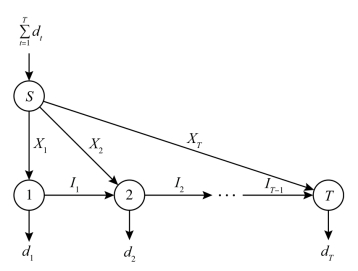
图1-2　基本DLS问题的网络流图示

在图1-2中，点{S}为问题的虚拟起始点，其流入量为问题在规划期T内的总需求。点集{1，2，…，T}对应1→T期，时期t节点上的流出量为该期需求dt。弧（S，t）上对应的流表示t期的订购量Xt，弧（t，t+1）上的流则为第t期末的持有库存It。基本的决策问题就转变为在这样一个凹性成本网络流中找到一个使总成本最小的极流（extreme flow）。对每个时期节点{t}来说，同时有两条弧流入，对应的流量分别为订购量Xt和持有库存量It-1。而根据单起点凹性成本网络流的性质“每个节点至多只能有一条弧流入量为正”，Zangwill直观地验证了零库存点订购性质，即It-1·Xt＝0。

基本DLS问题的另一主要拓展研究方向是该问题的解决方法。最初，Wagner和Whitin（1958）基于逆序动态规划的思想，设计了时间复杂度为O（T2）（其中T为问题的总规划期数）的精确求解算法，简称Wagner-Whitin算法。该算法在求解小规模（即计划期数T相对较小）问题时，效果较好，但当问题规模变大时，则效率会大大降低。而且，动态规划的算法在实际应用中较难理解，不便于实施。于是，一些学者提出了便于实施且行之有效的启发式算法，如著名的Silver-Meal算法。此外，还有一些学者致力于设计时间复杂度更低的精确多项式算法，但这一方面的研究颇为困难，因为最初的动态规划算法时间复杂度O（T2）已经足够低。直到DLS问题被提出30多年后，Federgruen等（1991）才提出了时间复杂度为O（TlogT）的算法来解决基本问题，并证明在无投机目的的成本条件下，即t期单位生产成本与单位库存持有成本之和不小于下一期t+1的单位生产成本（pt+ht≥pt+1）时，问题可以由其算法在线性时间O（T）内解决。随后，Wagelmans等（1992）和Aggarwal等（1993）分别采用几何解释（geometrical interpretation）蒙赫阵列（Monge array）的方法对问题进行分析，也设计出了时间复杂度为O（TlogT）的精确算法。

DLS问题与企业中的生产计划和库存管理密切相关，其对应的模型也是物料需求计划（material requirement planning，MRP）系统和高级计划系统（advanced planning system，APS）中的核心模块。MRP和APS在实际中的广泛应用和发展也推动了学界对DLS问题的深入研究。因此，围绕着基本问题的设定，学者们拓展研究了许多不同背景和应用环境下的问题。其中，最基本的拓展是考虑延迟交货（backlogging）的情况，即允许某一时期t的需求dt不被立即满足，而由t期之后的某期生产来满足，但延迟满足则会产生相应的惩罚成本。Zangwill（1966）最早研究了该问题并设计了一个时间复杂度为O（T3）的精确求解算法。后续学者们在提出一个新的DLS问题时，通常都会考虑不允许延迟交货和允许延迟交货这两种情形，并分别构建模型，设计求解算法。

多层级（multi-level/multi-echelon）环境下的DLS问题和有能力约束（capacitated）的DLS问题则是另外两个重要的拓展方向。前者是指在一个供应链环境中，最终产品需要在不同层级的设施中进行序列加工或生产，面对最终产品的确定性需求，决策者需要制订在不同层级的生产计划。Zangwill（1969）最先研究了该问题，并采用网络流的方法构建模型，设计了一个基于动态规划的精确求解算法。有能力约束的DLS问题包括两大类：一类是考虑生产能力约束的问题，一般体现在对t期生产量Xt的限制上；另一类则是考虑库存容量约束的问题，即对It的限制。Florian和Klein（1971）最先提出了凹性成本环境下有生产能力约束的DLS问题，采用网络流的方法分别为允许延迟交货和不允许延迟交货的情形构建了模型，并为恒定生产能力约束下的问题设计了时间复杂度为O（T4）的精确动态规划算法。Love（1973）则最先提出存在库存容量约束的DLS问题，并将此类问题同生产能力约束下的DLS问题进行了比较分析。Bitran和Yanasse（1982）研究了有能力约束的DLS问题在不同成本结构下的计算复杂性，并总结了哪些情况下的问题可以得到多项式求解算法，而哪些特殊情形下的问题是非多项式可解的，即NP-hard问题。

鉴于DLS问题在实际生产和库存计划中的基础地位，学者们结合不同的应用背景提出了许多其他定制化的拓展研究问题。例如，Sandbothe和Thompson（1990）在有生产能力约束的情况下，考虑企业策略性地不满足部分需求，第一次提出了允许缺货或销售损失的DLS问题，并设计了前进算法解决问题。一些学者在实际企业运营和营销部门联合决策的背景下，提出了DLS补货和定价同时决策的问题。面对实际企业需求信息随时间不断更新变化的情况，Baker（1977）提出了滚动计划期（rolling horizon）下的DLS决策方案，即确定一个计划周期，根据基本DLS模型和方法获得决策计划，但只实施第一期决策，随时间推移到下一需要决策的时期时再由新的需求信息来做下一个DLS决策，如此反复。Lee等（2001）根据第三方物流的合同交货特征，即有最早和最晚交货时间，抽象为考虑需求时间窗的DLS问题，并为无延迟交货的问题设计了一个时间复杂度为O（T2）的精确算法，为存在延迟交货的问题设计了复杂度为O（T3）的算法。另外，还有研究考虑当库存持有成本与存储时间相关时，库存存在变质情况下的DLS问题；面对着不同成本结构的多种生产或补给方式时，考虑如何选择生产方式和确定相应生产量的DLS问题；在确定性模型的基础上考虑不确定性因素，引入安全库存的DLS问题；以及带有成本学习效应的DLS问题，等等。在这些不同的DLS问题的分支领域，又有许多相关拓展研究，如考虑前文所提的延迟交货因素、多层级环境和能力约束等。当提出一个新的DLS问题后，通常要对问题的性质和结构进行分析，以期能够设计得到多项式时间的精确求解算法。但是，有些问题却是非多项式可解的，即NP困难（NP-hard）问题。此时，需要一些松弛近似算法或启发式智能算法来解决问题。Florian等（1980）就对确定性环境下的DLS问题进行了归类，总结出了多项式可解的问题和一些NP困难的特殊问题。

针对网络零售商部分商品的需求确定性较高且能提前获取的特点，本研究考虑了有完美提前需求信息（advance demand information，ADI）的动态批量补货问题，这和已有文献中带有需求/配送时间窗的DLS问题相近。接着，本研究结合著名B2C零售商亚马逊（Amazon）的“预判发货”（anticipatory shipping）专利背景，考虑了两种配送模式的批量发货问题，这与已有文献中考虑多种补货方式的DLS问题研究密切相关。因此，接下来本小节将重点对考虑时间窗的DLS问题和多种补货/发货模式的DLS问题进行介绍。(www.xing528.com)

1.考虑时间窗的动态批量问题

在确定性动态批量补货的相关文献中，有一些是专门研究带有时间窗约束的问题，进一步又可分为生产时间窗约束问题和配送时间窗约束问题。Lee等（2001）最先考虑有配送时间窗（又称需求时间窗）的动态批量补货问题，他们考虑的配送时间窗是指每一顾客需求都对应一个配送时间窗，即有最早交货期和最晚交货期，且在该时间窗内交付不会产生成本。例如，若某i类需求di对应的时间窗为[Ei，Li]，则该需求最早可以在Ei时期被满足，最晚满足时期不能超过Li。随后，Dauzère-Pérès等（2002）提出了生产时间窗问题，即生产/补货有一个最早启动时间和最晚启动时间约束。在该问题中，需求dk对应一个生产时间窗[Ek，Lk]，生产/补货必须最早在Ek时期进行，最晚不能超过Lk，而需求则在时期Lk得到满足。于是，若都用[Ei，Li]来表示需求di对应的配送时间窗和生产时间窗，二者的区别见表1-1。

表1-1　配送时间窗和生产时间窗的区别

考虑配送时间窗的动态批量问题在科技产品行业、服装业，尤其是第三方物流行业中非常适用。Lee等（2001）就是基于第三方物流业中订单“指定期限交付”的背景最先提出了考虑需求时间窗的DLS问题，并分别为无延迟交货和有延迟交货的问题设计了时间复杂度为O（T2）和O（T3）的精确算法。在随后十多年的时间里，学者们在其基础上拓展研究了不同背景下的考虑配送时间窗的动态批量问题。例如，Jaruphongsa等（2004）就从最基本的多级环境和能力约束两方面进行拓展，研究了在供应商管理库存（vendor managed inventory，VMI）或第三方物流配送环境下考虑需求时间窗的两级动态批量问题和有仓库容量限制的问题，并通过最优性质分析分别得到了复杂度不同的多项式时间精确求解算法。Hwang和Jaruphongsa（2008）则以半导体行业为研究背景，同时考虑有时间窗约束的主要需求和需要当期立即满足的次要需求，并设计了时间复杂度为O（n2T2）的最优算法，其中n为主要需求的种类，T为问题的总规划期数。在Lee等（2001）最初提出的问题中，成本结构是不允许投机的，而Hwang和Jaruphongsa（2006）则专门研究投机成本结构下的问题，根据非传统分解原则，设计了复杂度为O（nT3）的最优算法。另外，Hwang（2007）重新考虑Lee等（2001）提出的允许缺货的问题，为一般成本结构下的问题重新设计了更有效率的最优算法，使时间复杂度降低到O（max{T2，nT}），其中n为需求类别数目。Akbalik和Penz（2011）在单产品有能力约束的动态批量问题中比较了JIT政策（顾客需求只能在最后到期日满足）和配送时间窗政策，并指出这两种政策下的问题都是NP难题。Hellion等（2014）在一个企业和多个供应商之间存在稳定合同（stability contracts）的情况下探讨了更为复杂的动态需求时间窗的问题，并推测其为NP-hard问题。

考虑生产时间窗的动态批量问题通常来自生产取决于原材料或半成品可得性的系统环境，以及需求作为输入而非输出的环境，如工业废水处理行业。问题特征表现为需求有一个释放/可得期和交付期，前者是指需求被提出的时期或生产产品的原料到达的时期，后者则为需求被得到满足的指定时期。Dauzère-Pérès等（2002）最先提出了考虑生产时间窗的动态批量问题，并考虑两种时间窗结构：一种为无约束的时间窗结构，对应问题称为customer-specific（CS）problem；另一种为有约束的时间窗结构，即任意两类需求的时间窗不能有任何重叠，对应问题称为noncustomer-specific（NCS）problem。在他们的研究中，CS问题被证明是弱NP难题，可由一个指数时间的动态规划算法求解，而NCS问题则是多项式可解的，他们也设计得到了一个时间复杂度为O（T4）的精确算法。随后，Wolsey（2006）同时研究了考虑配送时间窗与生产时间窗的动态批量问题，并通过多种混合整数规划模型探讨了两种问题之间的关系。Hwang（2007）从算法角度重新考虑基本的生产时间窗动态批量问题，为无投机目的成本结构下的问题设计了时间复杂度为O（TlogT）的精确算法，为存在投机目的的固定线性成本结构下的问题设计了复杂度为O（T4）的算法，而为最一般的凹性生产成本结构下的问题设计了复杂度为O（T5）的算法。Absi等（2011）探讨了在提前生产、延迟交货和损失销售三种情形下有生产时间窗约束的动态批量补货问题，并设计得到了动态规划求解算法。以上考虑生产时间窗的问题针对的都是单产品情境，Brahimi等（2006）最先研究了一个有生产时间窗的多产品动态批量问题，并同时考虑了生产能力约束。针对该NP难题，他们利用拉格朗日松弛（Lagrangian relaxation）技术将多产品问题分解成多个可由多项式算法求解的单产品时间窗问题，取得了非常好的效果。随后，Brahimi等（2010）又在该问题的基础上进一步考虑生产启动时间，并将基于拉格朗日松弛技术的启发式方法与商业智能软件比较，发现前者在求解速度和效率上都优于后者。另外，还有学者在多产品生产时间窗问题的基础上结合订单分解与分配，并采用基于粒子群优化（particle swarm optimization）的启发式方法解决问题（Pan等，2014）。Van den Heuvel和Wagelmans（2008）比较了多种动态批量补货问题，发现考虑生产时间窗的动态批量问题在建模上可以同考虑库存容量限制的问题、再制造环境下的问题和考虑累积能力约束的问题互相转化。

本书在网络零售环境中研究了考虑提前需求信息的动态批量问题。在基本的设置下，网络顾客下单购买商品时相当于提前告知了未来的需求信息，因为只有当订单被交付完成时，对应的需求才得到满足。从顾客下单日期到商家指定的交付期这段时间可以被看成是该需求对应的交付时间窗。商家可以选择在该时间窗内任一时期来交付订单以满足需求。因此，本书的研究和已有文献中考虑需求/配送时间窗的动态批量问题密切相关。然而，在实际网络零售中，顾客收货时间（即需求被满足时期）经常会晚于初始指定的日期。其中原因包括快递滞后这样的不确定性因素，也包括商家自身的策略性拖后行为。根据实际情况，本书研究的问题允许商家在指定交付期之后交付，但不可无限拖延，即有最大延迟时间约束。在现有相关文献中，允许延迟交货通常是指可以将需求拖后到问题规划期内的最后一期来满足，而本研究则提出了一个考虑最大延迟约束的新问题，在一定程度上丰富了该研究方向的内容。

2.多补货模式的动态批量问题

多补货模式的动态批量问题通常发生在产品可以通过多个供应商供给或者通过多种运输方式运送的情况下，面对多种不同供应提前期和成本的补货或发货方式，决策者需要在问题规划期内的每一期同时决策用何种方式进行补货或发货，每种方式的补货或发货量应该是多少。在多方式补货或发货的DLS问题中，每种方式的成本结构是研究的重点，因为它会直接影响到设计最优求解算法的性质。Jaruphongsa等（2005）最先提出了存在多种补货或发货方式的DLS问题，但只重点分析了双模式补货的特例。当两种发货方式都为固定启动（fixed set-up）成本结构时，通过最优性质分析，他们设计了一个时间复杂度为O（T2）的精确动态规划算法；当一种发货方式为多启动（multiple set-ups）成本结构，另一种为固定启动成本结构时，利用最短路方法，设计了一个复杂度为O（T3）的最优算法；而当两种发货方式都为多启动成本结构时，问题可由复杂度为O（T4）的最优算法解决。随后，Jaruphongsa等（2007）在Jaruphongsa等（2005）的基础上，进一步考虑了补货和发货同时进行的两级系统下的双模式批量问题，且只在发货过程考虑两种运送模式，其中，一种为固定启动成本结构，另一种为多启动成本结构。根据分析得到的最优性质，他们通过动态规划方法设计了复杂度为O（T5）的算法解决问题。上述研究重点探讨的都是双模式的问题，而Toledo和Shiguemoto（2005）则研究了一个允许延迟交货的多种生产模式下的动态批量问题。不过在该问题中，所有的生产中心都是平行且具有简单的固定启动成本结构，这大大降低了问题的复杂性，所以他们也直接利用了Zangwill（1969）的算法求解该问题。Ekᶊiolu（2009）则研究了更为一般形式的多模式批量问题，即每一种补货/发货方式都具有多启动成本结构（固定启动成本结构可看成是多启动成本结构的特殊形式）。他首先利用网络流的方法描述问题，然后采用混合整数规划构建模型，并通过重新定义决策变量对问题进行重新建模，在重构模型线性松弛对偶问题的基础上，设计了一个基于原始-对偶的算法有效地解决了初始问题。随后，Bai和Xu（2011）在该文献的基础上进一步考虑多供应商的批量问题，其中每个供应商对应的成本结构可以是增量折扣（incremental quantity discount）、多启动成本和全单位数量折扣（all-unit quantity discount）中的任意一种。他们指出，当所有供应商具有增量折扣或多启动成本结构时，问题可由基于动态规划的多项式算法求解；而当所有供应商的成本结构为全单位数量折扣时，则不能找到合适的多项式算法。Palak等（2014）则研究了一个考虑多模式补货和环保因素的影响，探讨了碳排放政策对不同补货模式选择的影响。

与多补货模式问题密切相关的还有两类动态批量问题：多启动（multi-setups）成本的动态批量问题；多阶段或序列的动态批量问题。多启动成本的动态批量问题是指在进行批量补货或发货时，交通运输工具通常有固定容量限制，比如卡车或集装箱的装载容积通常固定，每使用一单位这种交通工具时，除了要支付固定成本和单位货物运输成本，还需要额外支付对应的单位交通工具成本（即使该交通工具并没有装满货物）。该问题使得补货或发货的成本结构变得异常复杂，进而导致求解算法变得难以设计。在以上多模式批量问题的文献[59][79][81][82]中，多启动成本结构的情境都是作为重点分析的对象。多阶段或序列的动态批量问题是指在一个多阶段或序列的供应链系统中的批量补货和发货决策问题，前一阶段的输出通常是后一阶段的输入。Kaminsky和Simchi-Levi（2003）最先考虑了一个有生产和分发的两阶段供应链环境下的动态批量问题。在该问题中，无限供应的原材料要经过有能力约束的阶段一和阶段二的连续加工，才能成为最终产品，且阶段一的加工品需要通过交通方式运输到阶段二进行再加工。作者考虑了当阶段一和阶段二的生产成本以及它们之间的运输成本都是无投机目的时的特殊情形，并设计了多项式算法解决问题。Lee等（2003）在第三方物流背景中，考虑同时补货和发货的批量决策问题，且发货模式是多启动成本结构。随后，Jaruphongsa等（2007）在该问题基础上拓展，考虑发货过程存在两种不同成本结构的运输方式。Van Hoesel等（2005）则将问题拓展到多阶段序列供应链环境中，并考虑生产能力约束。在不同运输成本结构和库存持有成本结构的情况下，他们利用网络流的方法分析了问题的可解性，及相应的算法时间复杂度。还有学者在这种有能力约束的两阶段序列供应链中考虑额外补货方式的问题，如允许自己生产和外部采购（subcontracting）两种模式同时补货（Sargut和Romeijn，2007）。

在多补货模式动态批量问题中，只有每种补货模式存在不同的成本结构时，问题才会有意义。现有文献大多会假设其中的一种补货模式具有多启动成本结构，因为在实际中，多补货模式通常与交通运输相关，而该成本结构正符合采用固定容积交通工具来运输的情况。于是，在最优方案的求解中，就会存在多启动成本结构模式补货和其他成本结构（如线性成本、固定启动成本）模式补货的博弈问题，这就为性质分析和算法设计带来了困难，使整个问题具有挑战性。另外，多补货模式的动态批量问题通常被置于一个多阶段或序列的供应链系统中，它往往结合了补货和发货这两种决策问题，既可以考虑多种补货模式，也可以考虑多种发货（即运输）模式。已有文献中多层级间的发货或补货流是不可以越级的，即只能在相邻阶段或层级之间进行补货或发货活动。这使得动态批量问题中的关键性质——零库存点补货/发货性质大多成立，从而为分析最优性质和算法提供了便利。

本书基于网络零售商“预判发货”（anticipatory shipping）的应用背景，研究了在一个两层级供应链系统中的动态批量发货问题。当该网络零售商为其订单履行中心完成补货后，需要制订发货计划，以满足多期的客户需求。发货途径有两种：一种是通过自营物流配送将货品运输到配送站，之后由快递员从配送站配送至终端客户；另一种则是直接由第三方物流从履行中心发货给顾客。该问题的背景和相关文献中多补货/发货模式的批量问题一样，每种发货方式的成本结构是不同的。但不同的是，通过第三方配送的发货方式存在一个跨越二级库存的问题，即直接越过了配送站这一级。这使得原有文献中的性质分析和算法都不适用于该问题，给寻求解决问题的方法带来了新的挑战。