IEEE-9节点系统电压安全成本分析

该系统有3台发电机，9条线路，3个负荷，系统接线图如图3-15所示。

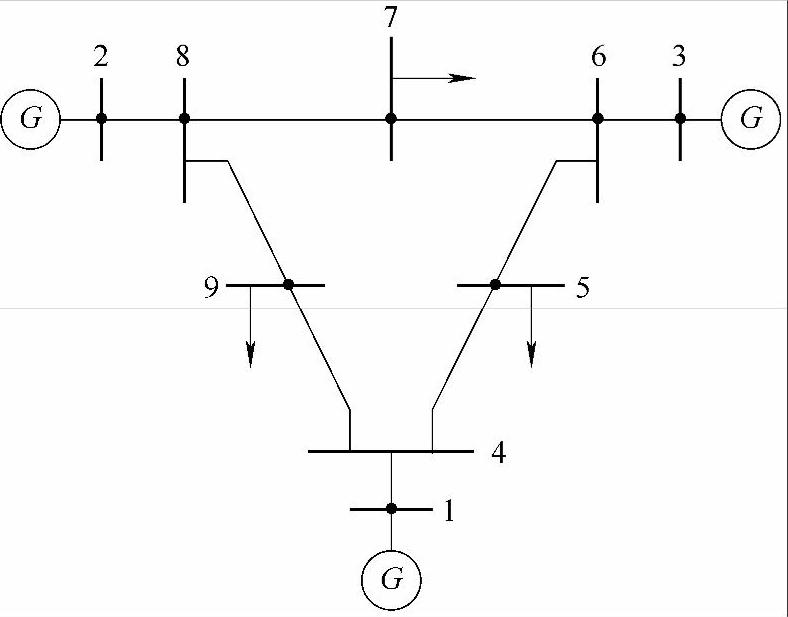
图3-15 IEEE-9节点系统接线图

本章参考文献[2]提供的节点电压约束为0.90p.u.～1.10p.u，为了将本书提出的计及理想负荷裕度范围的模糊多目标最优潮流模型应用于该系统，仿真计算取节点电压约束为0.95p.u.～1.05p.u。分别取理想负荷裕度下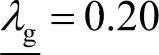限、上限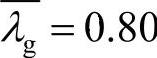，负荷裕度模糊参数δ_g1=0.01、δ_g2=0.10，节点电压模糊参数向量δ_s=0（n-N_G维零向量）（即此时不考虑对节点电压约束进行模糊化处理）；然后其他参数不变，取δ_s=0.05e（e为n-N_G维单位列向量）。

1.单目标最优潮流仿真结果比较

对应于不同负荷条件下、以系统总发电成本为优化目标的单目标最优潮流（在节点电压约束分别取0.90p.u.～1.10p.u.和0.95p.u.～1.05p.u.时）求得的系统最优发电成本如图3-16所示。注意这里的当前负荷水平d_p与前面定义相同。

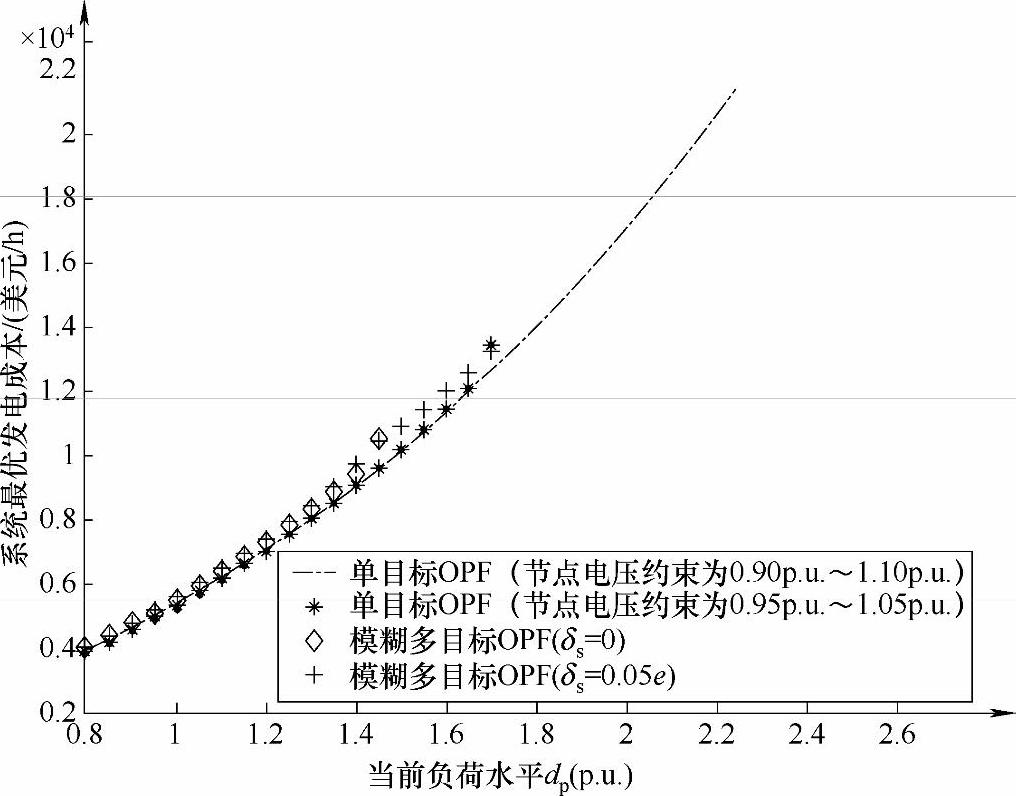
图3-16 IEEE-9节点系统对应于当前负荷水平d_p的系统最优发电成本

由图3-16可见，当节点电压约束取0.90p.u.～1.10p.u.时，直到当前负荷水平d_p=2.25，由单目标最优潮流仍然能够求得系统优化运行解，在此情况下得到的解有可能是“冒险”解。当节点电压约束取0.95p.u.～1.05p.u.时，在当前负荷水平高于d_p=1.70以后，由单目标最优潮流已无法得到系统的优化运行解，在此情况下得到的解可能是“保守”解。对应于同一负荷水平，两种节点电压约束下求得的系统最优发电成本，后者略高于前者，说明为了确保系统电压安全，系统的优化运行需要付出一定的经济代价。

由以上分析可知，将节点电压约束由0.95p.u.～1.05p.u.简单地松弛处理为0.90p.u.～1.10p.u，会使系统的优化运行解由“保守”解跳变到“冒险”解，不适于系统的实际优化运行，而将节点电压约束模糊化处理的模糊建模方法则可以克服两种约束条件下进行优化计算的不足，使优化运行解在“保守”解与“冒险”解之间寻求适当的折中。

2.模糊多目标最优潮流仿真结果比较

对于本书提出的计及理想负荷裕度范围的模糊多目标最优潮流模型，以0.95p.u.～1.05p.u.作为系统节点电压约束，图3-16和表3-1同时给出了未对节点电压约束进行模糊化处理（δ_s=0）和对其进行模糊化处理（δ_s=0.05e）的优化结果。由表3-1可知，当δ_s=0时，对于当前负荷水平d_p＞1.45的负荷条件下，不存在最优运行解；而当δ_s=0.05e时，在当前负荷水平d_p＞1.70以后，才无法得到系统的优化运行解。

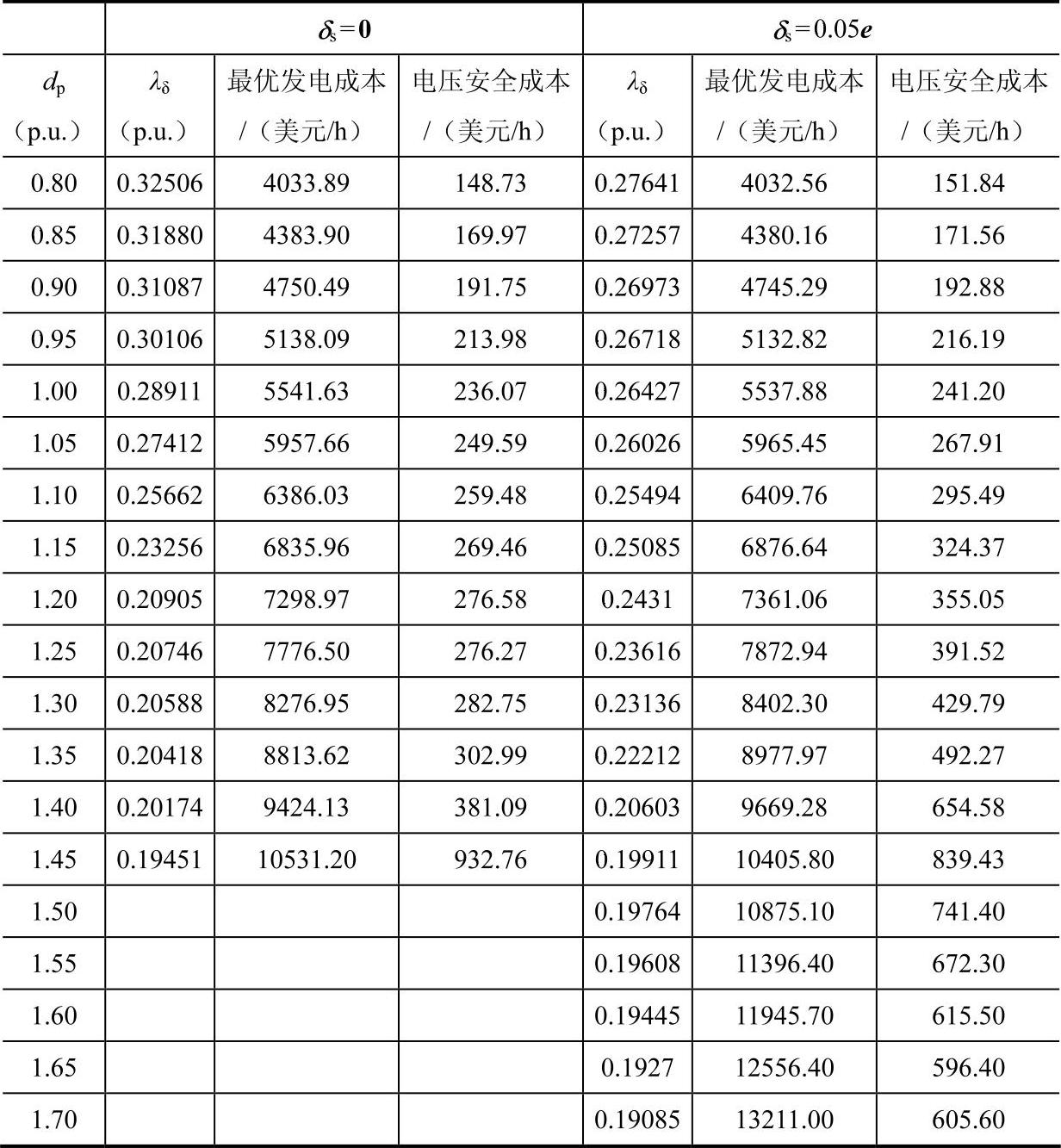
比较单目标最优潮流与模糊多目标最优潮流优化结果可以发现，当考虑系统的电压安全裕度时，对应于同一负荷水平下，系统优化运行的最优发电成本有所增加；而且当负荷水平升高到一定程度后，单目标最优潮流仍可得到最优运行解，考虑电压安全裕度的模糊多目标最优潮流已经无法得到最优运行解。一方面表明系统优化运行为了维持一定的电压安全裕度，需要额外耗费一部分发电成本；另一方面表明，随着系统负荷水平的升高，当系统优化运行后的实际负荷裕度无法达到模糊化后的理想负荷裕度下限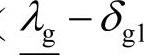（）时，该负荷条件下不存在优化运行解。

比较表3-2中δ_s=0和δ_s=0.05_e两种情况下的优化结果发现，当前负荷水平d_p介于0.80～1.00之间时，系统最优发电成本前者略高于后者，而当前负荷水平d_p介于1.05～1.40之间时，系统最优发电成本前者略低于后者，这正反映了模糊多目标最优潮流模型能够在几个优化目标（系统总发电成本、系统电压安全裕度指标和节点电压幅值）之间寻求最佳的平衡点。(www.xing528.com)

表3-2 IEEE-9节点系统对应于不同负荷条件下的模糊优化结果比较

参照δ_s=0的情况，可以分析在δ_s=0.05e的情况下，相比较而言，系统最优发电成本先低于后高于前者的原因。在当前负荷水平d_p≤1.00时，为满足经济性要求，可允许系统节点电压稍微越限且运行于较低的实际负荷裕度，因此，得到的系统最优发电成本略低于同一负荷水平下δ_s=0（不允许节点电压越限）的情况；在当前负荷水平d_p≥1.05时，对于δ_s=0.05e的情况，为了在节点电压幅值、系统电压安全裕度指标以及系统最优发电成本三个目标之间寻求最佳平衡点，尤其在负荷水平d_p≥1.15后，在获得实际负荷裕度较高于δ_s=0的情况的前提下，同一负荷水平下，δ_s=0.05e时得到的系统最优发电成本略高于δ_s=0的情况。

另外，由表3-2注意到，当对节点电压约束进行模糊化处理后，随着系统负荷水平的升高（d_p＞1.45），仍然存在最优运行解，但系统优化得到的实际负荷裕度并不因为对节点电压约束的模糊化处理而提高到处于理想负荷裕度范围内，仅仅是处于理想负荷裕度下限与模糊化处理后的理想负荷裕度下限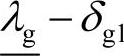（）之间。这表明节点电压约束是否进行模糊化处理与系统优化运行的电压安全裕度之间不存在必然的联系。

比较表3-2中的电压安全成本可以发现，当前负荷水平d_p=1.45时，两种δ_s取值情况下优化得到的系统电压安全成本都是最高的，分别为932.76美元/h（δ_s=0）和839.43美元/h（δ_s=0.05e）。对于δ_s=0的情况，随着当前负荷水平的升高，系统电压安全成本逐渐升高；而对于δ_s=0.05e的情况，随着当前负荷水平的升高，直到d_p=1.45，系统电压安全成本逐渐升高，在d_p＞1.45后，随着负荷水平的升高，系统电压安全成本逐渐降低。这表明当前负荷水平升高到一定程度后，由于系统各发电机的有功出力限制，已无法通过改变发电出力、付出更大的经济代价来提高系统的电压安全水平，即已经无法通过经济代价换取系统的电压安全，但通过优化得到的系统实际负荷裕度与电压安全成本两个指标可以反映系统优化运行的电压安全性。这同样能给系统运行人员和市场参与者以警告，使其共同采取配合措施，以降低系统发生电压失稳的可能。

对应于同一负荷水平，比较δ_s=0和δ_s=0.05e两种情况下的系统电压安全成本可以发现，后者的电压安全成本高于前者的电压安全成本（除了d_p=1.45的情况），表明节点电压约束是否进行模糊化处理，对系统优化运行的电压安全成本有一定的影响，模糊化处理后的系统电压安全成本稍微有所增加。

图3-17和图3-18分别示出了模糊优化模型求得的对应于不同负荷条件下的系统实际负荷裕度和系统电压安全成本。

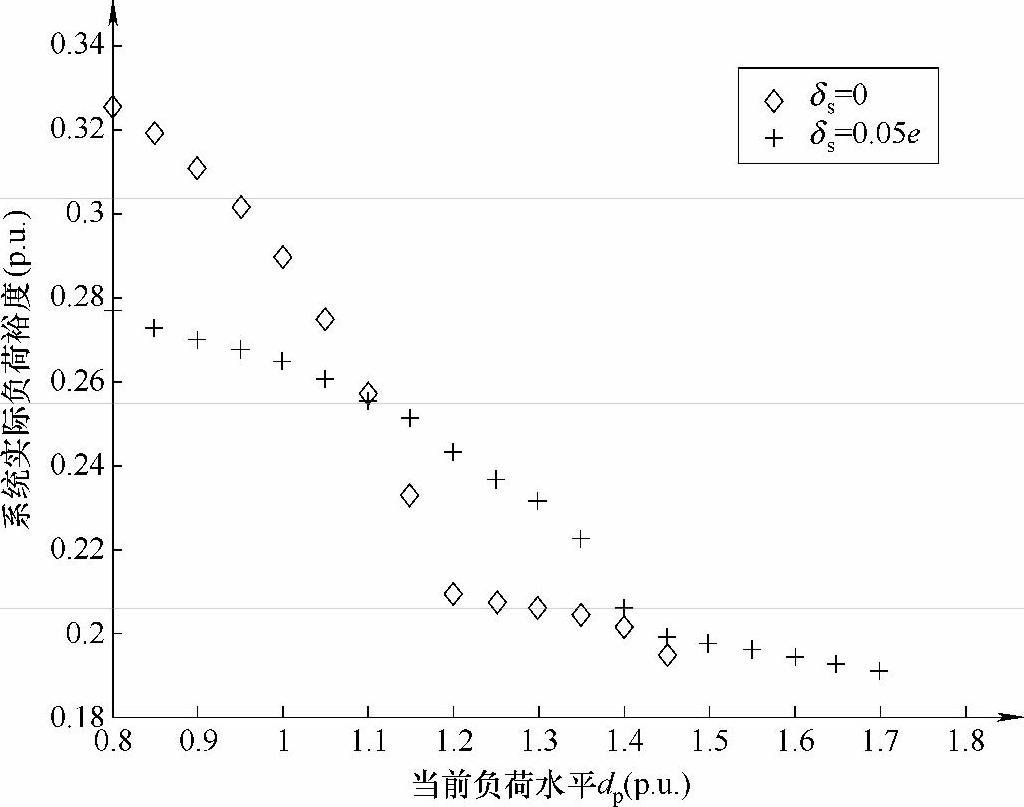
图3-17 IEEE-9节点系统对应于当前负荷水平d_p的系统实际负荷裕度

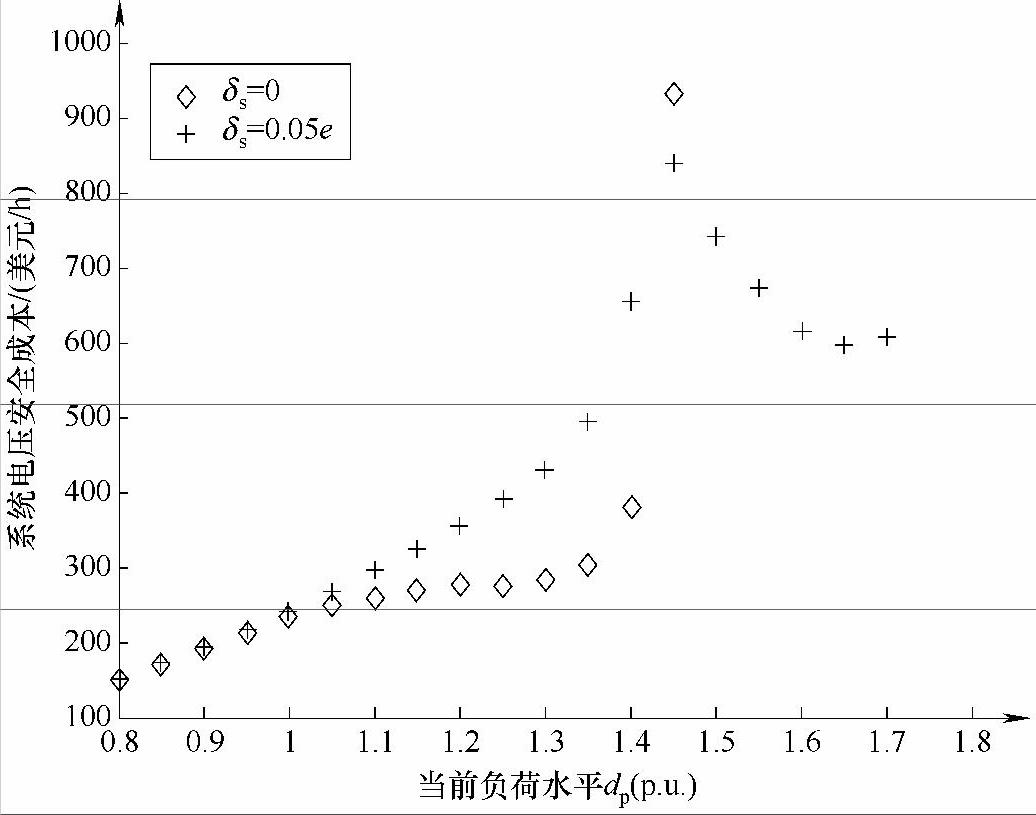
图3-18 IEEE-9节点系统对应于当前负荷水平d_p的系统电压安全成本

由图3-17可见，在δ_s=0.05e的情况下，系统优化得到的实际负荷裕度随着负荷水平的升高变化比较平缓，而在δ_s=0的情况下，则随着系统负荷水平的升高，优化得到的实际负荷裕度下降较快。

在系统实际运行中，运行人员可在本书给出的理想负荷裕度上、下限定义的基础上，根据系统特点确定适合该系统的理想负荷裕度范围，并可针对不同运行情况改变模糊参数值，据此可以通过该算法实现对系统运行状态的分析与控制，并获得相应的系统电压安全成本。