校正原对偶内点法优化预测问题求解

根据原对偶内点法求解最优潮流问题的主要步骤，先引入松弛变量将不等式约束转换成等式约束，再用对数障碍函数将松弛变量作为软约束加入目标函数，最后通过将所有约束加入改进的目标函数而形成拉格朗日函数，即

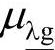式中，为障碍参数；其他的µ包括变量、、、、和向量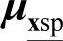、、、、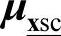、、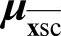、、、、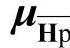、、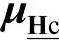、、、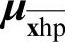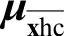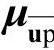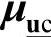以及γ_p，γ_c∈RM为拉格朗日乘子向量，对应于μ的s（s_i≥0，∀i）为松弛变量向量。这样，约束优化问题就转换成了无约束优化问题。

根据Kuhn-Tucker最优性条件可得：

式中，e₁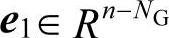（）、e₂（e₂∈R^nline，nline表示系统线路数）、e₃（e₃∈R^N-n+NG）、e₄（e₄∈R^M）均为单位列向量；S_i（对任意的i）表示以向量s_i的元素为对角元素的对角矩阵。

对式（3-45）～式（3-94）构成的非线性方程组用牛顿法求解，可得各变量的修正方程式为

式中，z=（x_p，c，u_p，c，λ_δ，η）T表示原变量向量；向量s包括所有的松弛变量，矩阵S是以向量s的对应元素为对角元素的对角矩阵；e是单位列向量（其维数等于不等式约束数）；μ包括所有不等式约束对应的拉格朗日乘子；γ包括γ_p和γ_c；F表示当前运行点和临界运行点的节点潮流方程；W表示增广海森矩阵，其元素是拉格朗日函数L对所有变量的二阶偏导数。

Mehrotra提出将原对偶内点法扩展为预测-校正原对偶内点法。预测-校正原对偶内点法与纯粹的原对偶内点法的主要区别是在式（3-45）～式（3-71）中引入非线性项。加入非线性项（二阶项）后，式（3-95）变为

式中，∆S表示以∆s的对应元素为对角元素的对角矩阵。预测-校正法先执行一个障碍参数置为0的仿射步[即令式（3-95）中的μ_s为0]，然后由仿射步所得的结果计算障碍参数和二阶项及上式中等式右边的各项，再求解式（3-96）得到校正后的各变量的修正量。该方法虽然每次迭代的计算量稍有增加，但由于具有更成功的搜索方向，使得总的迭代次数和求解时间大大减少。

采用预测-校正原对偶内点法求解3.7.1节优化问题的算法步骤如下：(www.xing528.com)

1）初始化。读入系统数据和初始潮流数据；设置最大迭代次数，令k=0；设置变量和参数的初始值，令安全因子σ=0.95，中心参数τ=0.2；将优化过程的收敛判据设为：①障碍参数μ_s小于10^-10；②当前运行点与临界运行点的各节点潮流偏差中最大的偏差量小于10^-4；③增量向量∆z、∆γ_p和∆γ_c中最大的元素小于0.005；④与上次迭代的目标函数值相比，目标函数增量的绝对值小于0.005·（1+η）。

2）令μ_s=0，由式（3-76）可求得第k次迭代仿射步各变量的修正量，根据求得的松弛变量和对偶变量的修正量，可确定第k次迭代仿射步原变量和对偶变量的修正步长α_p^k和α_d^k分别为

3）计算第k次迭代仿射步补偿间隙C^k_{gap_af}=（s^k+α_p^k·Δs^k）^T（µ^k+α_p^k⋅Δµ^k），令C^k_gap=（s^k）^Tµ^k，则可用下式估计障碍参数µ_s^k：

式中，p表示式（3-72）～式（3-92）的方程个数（即为不等式约束数）。

4）计算Sµ-µ_se+ΔSΔµ，进入校正步。

5）用含有二阶项的Sµ-µ_se+ΔSΔµ代替仿射步的Sµ-µ_se，计算式（3-96）得到第k次迭代校正后的各变量的修正量。

6）重新应用式（3-97）和式（3-98）计算修正步长α_p^k和α_d^k，更新变量。

7）判断是否满足收敛判据，若满足，则停止迭代，输出优化结果；否则，k=k+1，转步骤2）。