美国控制理论专家L.A.Zadeh于1965年引入了“模糊”的概念,给出一组变量X={x},关于X的模糊集合C定义为一组有序数对C={(x,μC(x))|x∈X},μC(x)是x的隶属函数,其值在[0,1]之间,μC(x)的值越大,x属于C的可能性越大;如果μC(x)限定为0或1,则C为非模糊集。另外,如果模糊集A和B的隶属函数分别为μA(x)和μB(x),则A与B的交集D的隶属函数可定义为
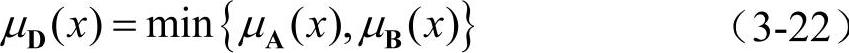
由以上定义可见,在多目标规划问题中,具有不同量纲的目标函数与可松弛约束只要能确定其相应的隶属函数,就可以式(3-22)的形式表示它们的交集,从而将多目标规划问题的解定义为目标函数与可松弛约束集合的交集,使该优化问题转换成交集的最大化问题。
因此,多目标最优潮流模糊建模的关键在于隶属函数的确定。对于式(3-20)的多目标规划问题,理论上总希望在满足所有硬约束以及最大限度地满足可松弛约束(节点电压约束)条件下,系统的总发电成本越少、实际负荷裕度偏离理想负荷裕度范围越少越好。目标函数分量g(xp,up,Ap)、Md和可松弛变量向量xs的隶属函数可分别由以下分段线性函数表示:
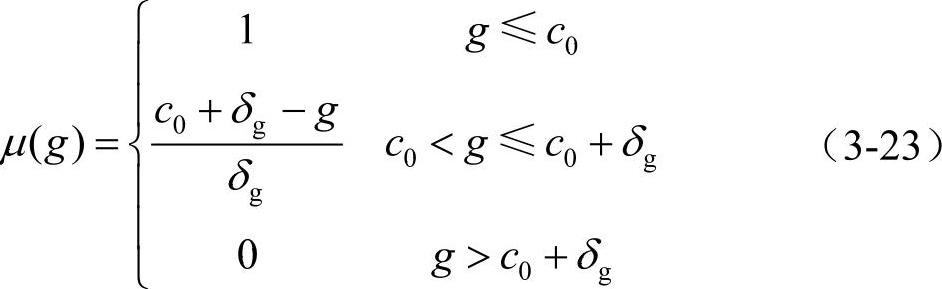
式中,为了表示方便,将系统总发电成本函数g(xp,up,Ap)表示为g;c0+δg表示最高可接受系统总发电成本,这里取优化前的系统总发电成本,则最小发电成本就由期望的最大发电成本节约δg来决定。
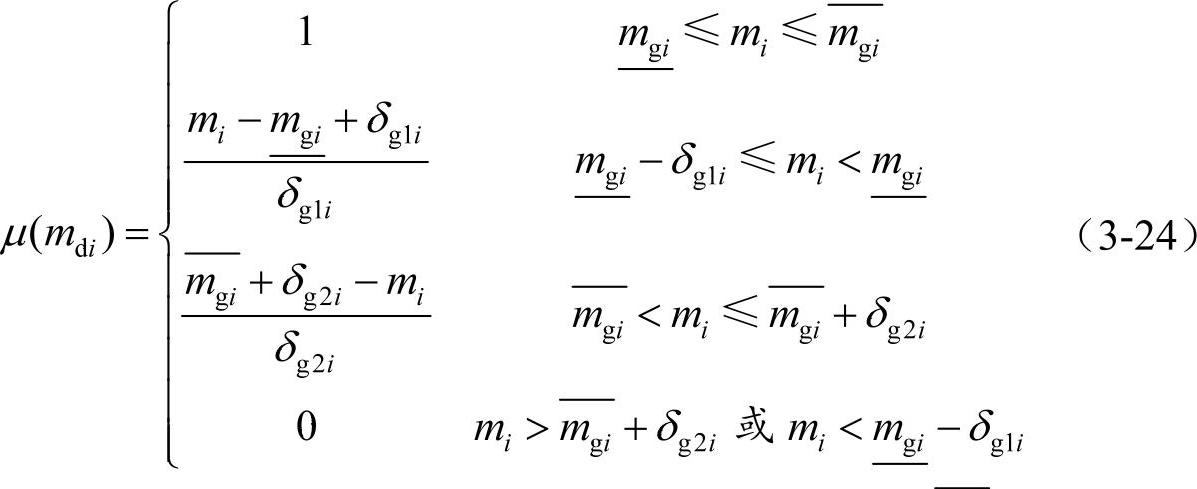
式中,mi(i=1,2,…,2l)为向量M中的第i个元素;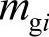 和
和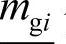 分别为向量Mg和
分别为向量Mg和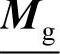 中的第i个元素;δg1i和δg2i分别表示对应于理想负荷裕度下限和上限的负荷裕度模糊参数;mdi表示向量Md中的第i个元素。
中的第i个元素;δg1i和δg2i分别表示对应于理想负荷裕度下限和上限的负荷裕度模糊参数;mdi表示向量Md中的第i个元素。
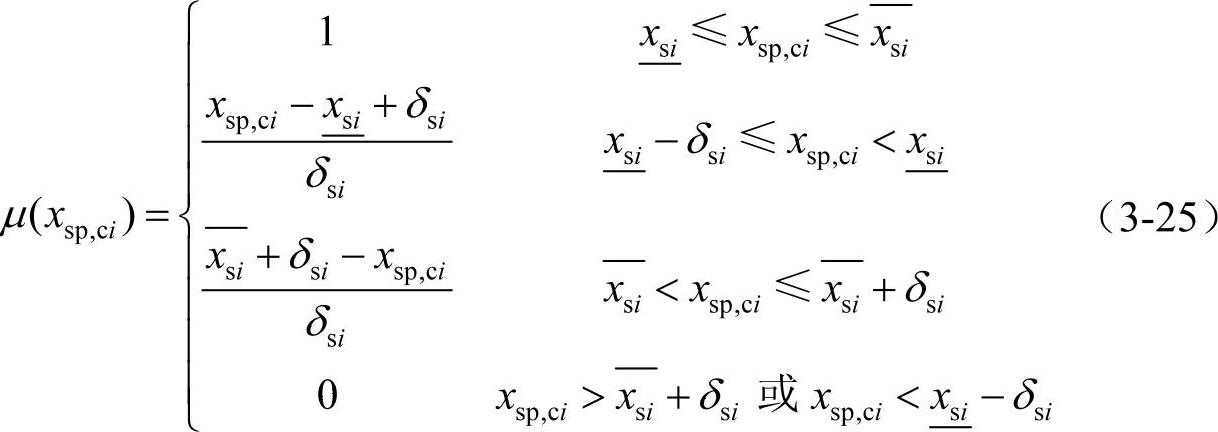
式中,xsp,ci(i=1,2,…,n-NG)为向量xsp,c中的第i个元素;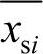 和
和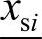 分别为向量
分别为向量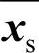 和
和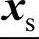 中的第i个元素;δsi表示第i个节点电压模糊参数,注意这里的节点电压上限与下限取了相同的模糊参数,也可以根据系统运行的实际情况,采用
中的第i个元素;δsi表示第i个节点电压模糊参数,注意这里的节点电压上限与下限取了相同的模糊参数,也可以根据系统运行的实际情况,采用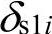 和
和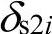 分别表示对应于节点电压下、上限的模糊参数,以更自由地确定下、上限的最大越限量;该隶属函数的表达式说明系统非发电机节点电压幅值可以稍微越限,但越限越多,越不可接受。
分别表示对应于节点电压下、上限的模糊参数,以更自由地确定下、上限的最大越限量;该隶属函数的表达式说明系统非发电机节点电压幅值可以稍微越限,但越限越多,越不可接受。
对应于以上隶属函数的分布曲线分别如图3-12、图3-13和图3-14所示。(https://www.xing528.com)
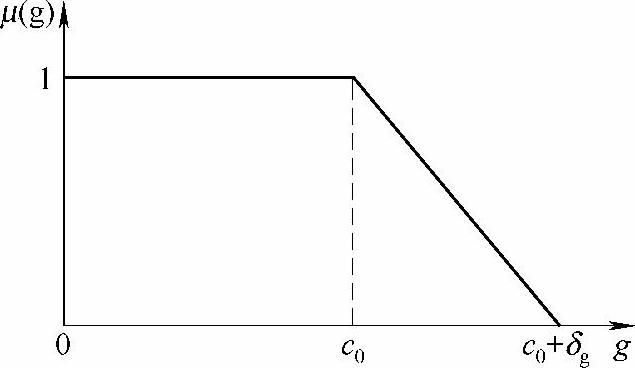
图3-12 发电成本g的隶属函数分布曲线
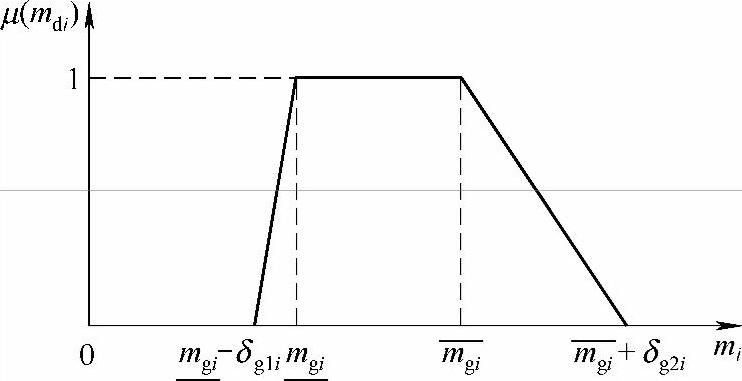
图3-13 mdi的隶属函数分布曲线
在图3-13中,当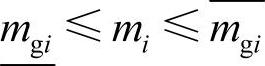 时,即当系统实际负荷裕度在期望的理想负荷裕度范围内时,隶属函数为1,两边向下倾斜部分表示实际负荷裕度超出理想负荷裕度范围越多,越不可接受。取负荷裕度模糊参数δg1i<δg2i,原因是当系统实际负荷裕度比最小理想负荷裕度小得比较多时,系统运行越接近其电压稳定极限,容易发生电压失稳而无法满足安全性要求,为造成巨大社会经济损失带来隐患,这是系统运行绝对避免的现象,因此参数δg1i应根据系统具体情况选一个非常小的量,而当系统实际负荷裕度比最大理想负荷裕度大得比较多时,系统运行更加安全,只是系统的利用效率降低,无法满足经济性要求。但在某些特殊情况下(如系统负荷水平较低时),允许系统为了安全运行而丧失部分经济性,因此理论上δg2i取的应比δg1i稍大一些。
时,即当系统实际负荷裕度在期望的理想负荷裕度范围内时,隶属函数为1,两边向下倾斜部分表示实际负荷裕度超出理想负荷裕度范围越多,越不可接受。取负荷裕度模糊参数δg1i<δg2i,原因是当系统实际负荷裕度比最小理想负荷裕度小得比较多时,系统运行越接近其电压稳定极限,容易发生电压失稳而无法满足安全性要求,为造成巨大社会经济损失带来隐患,这是系统运行绝对避免的现象,因此参数δg1i应根据系统具体情况选一个非常小的量,而当系统实际负荷裕度比最大理想负荷裕度大得比较多时,系统运行更加安全,只是系统的利用效率降低,无法满足经济性要求。但在某些特殊情况下(如系统负荷水平较低时),允许系统为了安全运行而丧失部分经济性,因此理论上δg2i取的应比δg1i稍大一些。
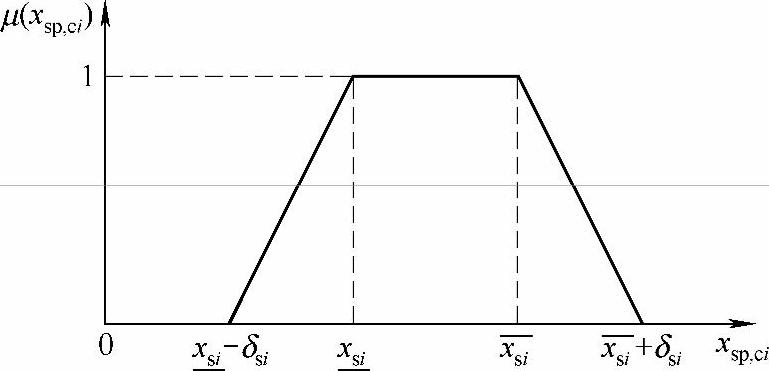
图3-14 xsp,ci的隶属函数分布曲线
令η为式(3-23)~式(3-25)中所有隶属函数中最小的隶属变量,可称之为满意度,即
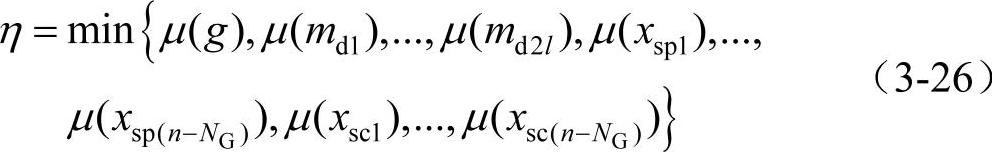
由此,原问题可转化为使满意度η最大化的单目标最优潮流问题。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




