分析IEEE-57节点系统仿真结果：优化方案

IEEE-57节点系统接线图如图3-1所示，表3-1给出了发电机

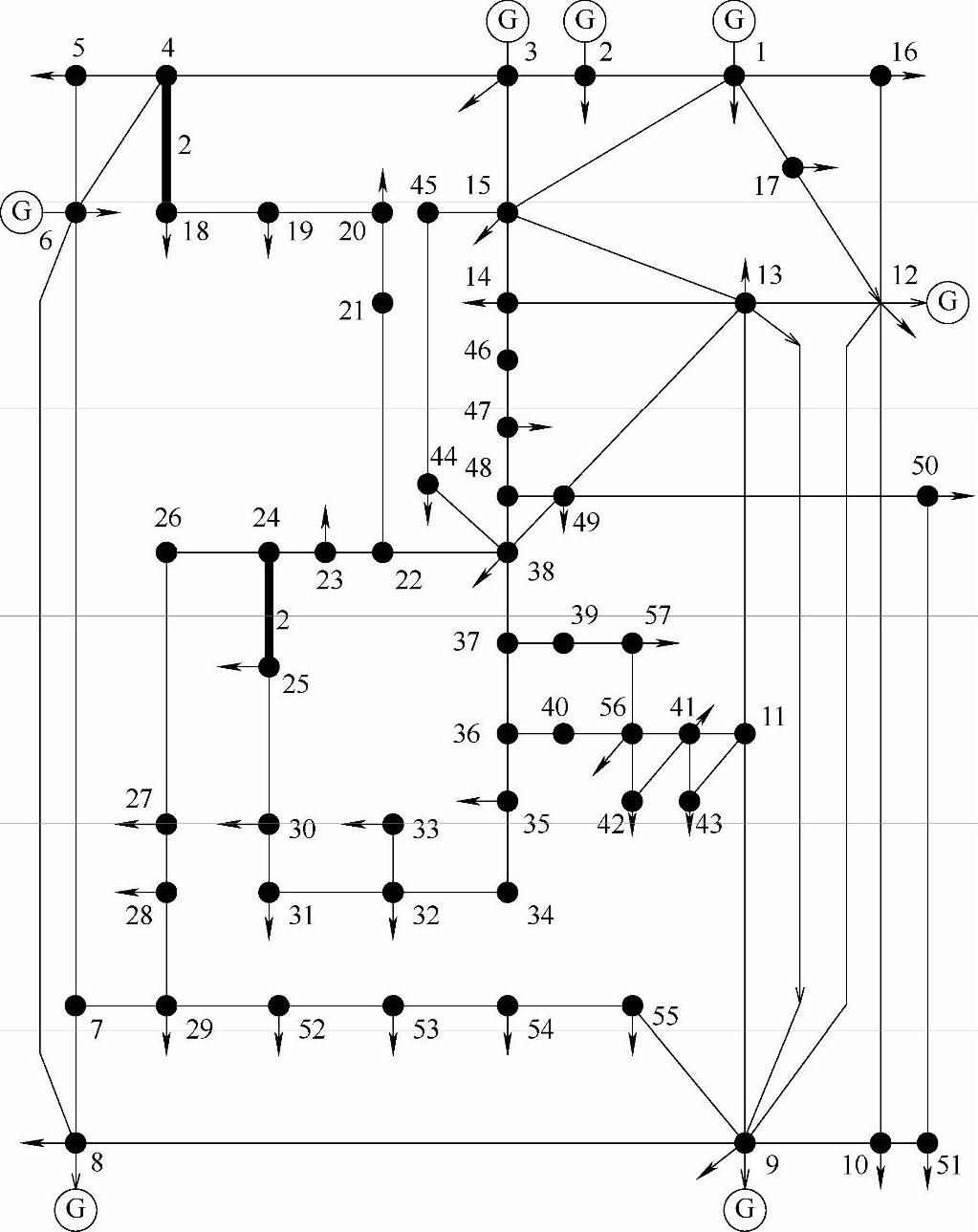
图3-1 IEEE-57节点系统接线图

的经济参数及初始有功出力与出力限值，系统其他数据可参考本章参考文献[2]。

表3-1 IEEE-57节点系统发电机的经济参数及初始有功出力与出力限值

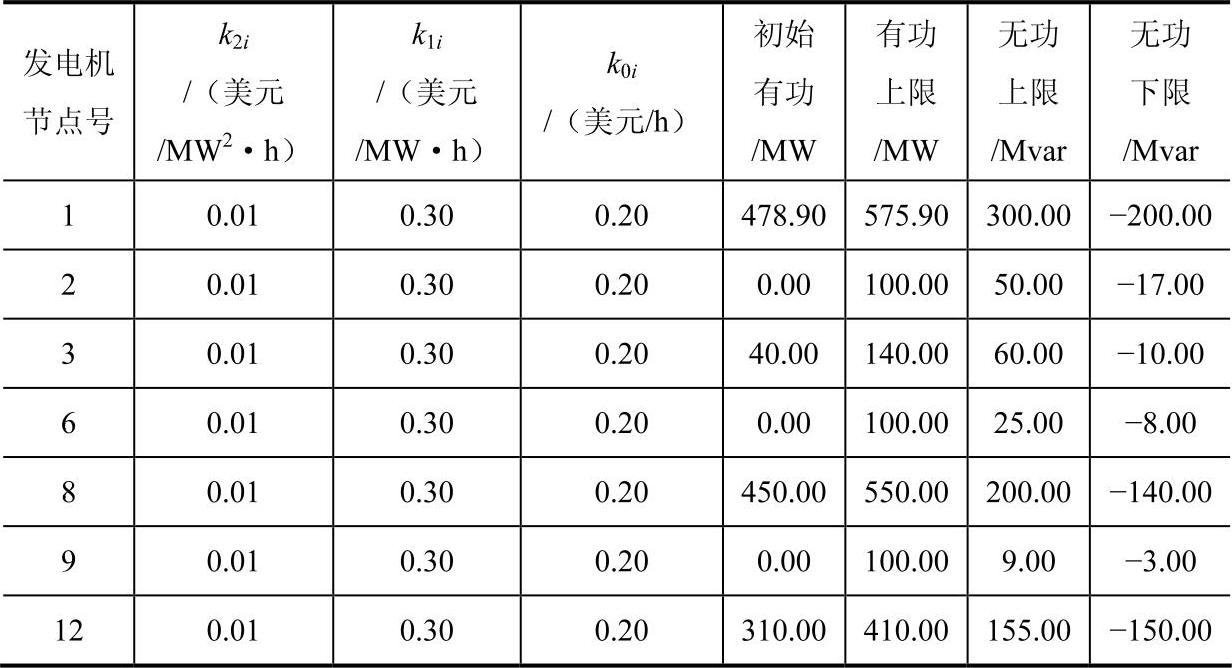
（1）系统电压稳定分析

利用连续潮流法^[1]分别得出不考虑任何系统限制以及考虑发电机无功功率限制时，对应于当前负荷水平d_p的系统临界负荷水平dc，如图3-2所示。负荷参数dp与dc是相对于测试系统给定的初始负荷水平而言，即将给定的系统初始负荷作为基准负荷A₀（A₀∈R^2l），当前负荷水平和临界负荷水平则可以分别表示为d_p·A₀和d_c·A₀（因为采用线性、恒功率因数增长的负荷增长方式）。在同一基准下，可简单地用负荷参数d_p与d_c表示，如未加特别说明，本研究的仿真分析都采用该表示方法。显然，考虑发电机无功功率限制对于系统的临界负荷水平有相当大的影响，即在同一负荷水平下，当考虑发电机无功功率限制时，对应于该负荷水平的临界负荷水平大大降低，这就是极限诱导分叉（Limited-Induced Bifurcation，LIB）形成的原因^[1]。

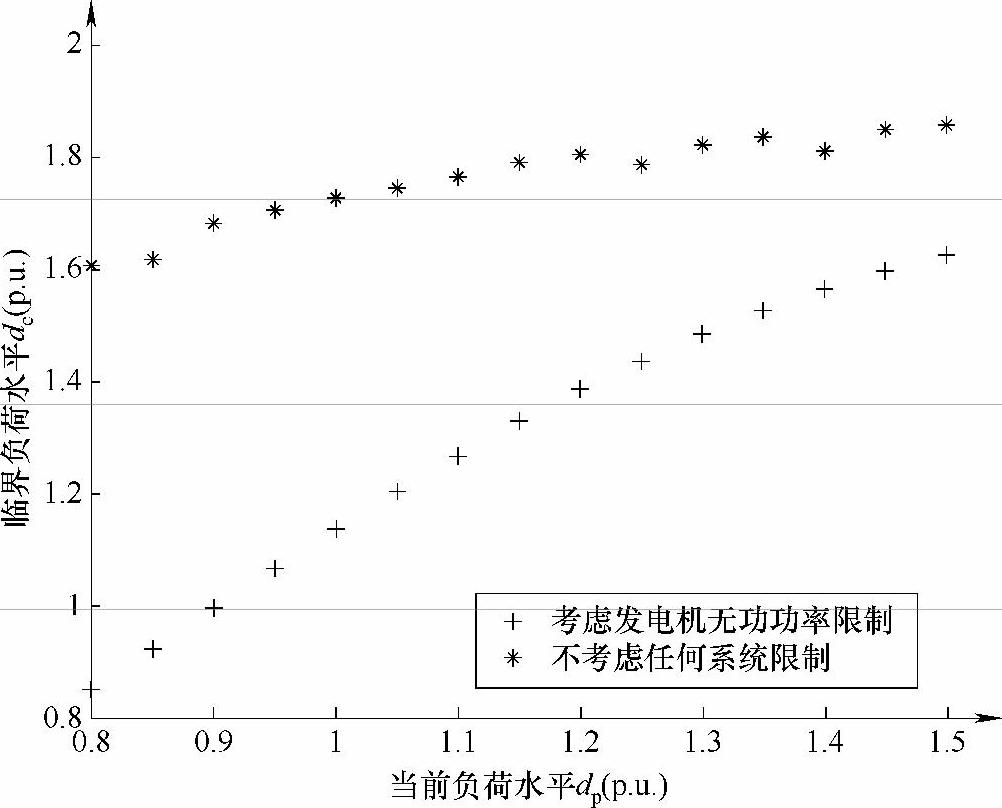
图3-2 IEEE-57节点系统当前负荷水平d_p与临界负荷水平d_c的关系

图3-3与图3-4分别给出了采用连续潮流法获得的基准负荷条件下、系统当前负荷水平d_p与某些特殊负荷节点电压的关系。

显然，图3-3与图3-4所示系统当前负荷水平与负荷节点电压之间的关系，与图2-1的系统网络结构有非常密切的联系。负荷节点16和17分别位于发电机节点1与12之间，使得系统电源对该节点的电压控制作用很强，几乎不受负荷增长的影响，节点电压始终保持在稍微高于额定值运行；而负荷节点25、30、31、32和33则离系统所有电源点都很远，其等效电距离与其他负荷节点相比最远，形成一个远距离负荷中心，使得系统电源对这些节点电压的控制作用大大减弱，从而其节点电压随着负荷增长大幅下降，如果不及时采取有效措施限制负荷，并就近规划投资电源建设，将会导致系统失稳甚至崩溃。

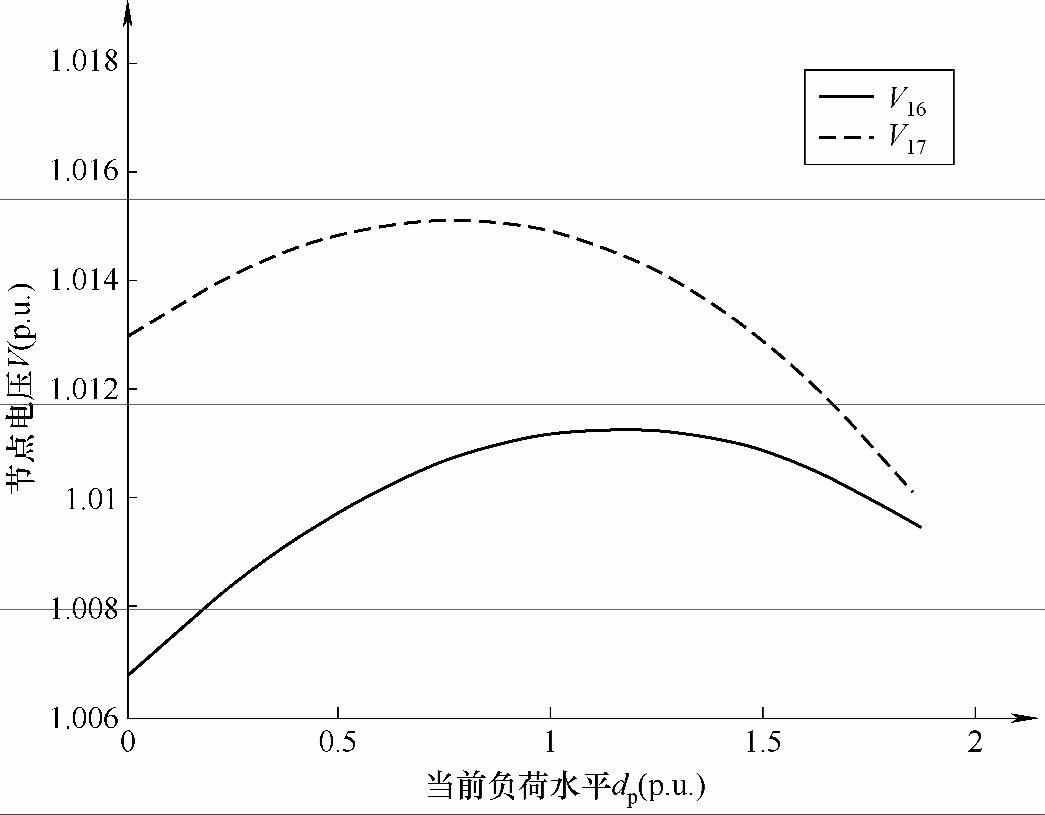
图3-3 IEEE-57节点系统当前负荷水平d_p与负荷节点电压V₁₆和V₁₇的关系

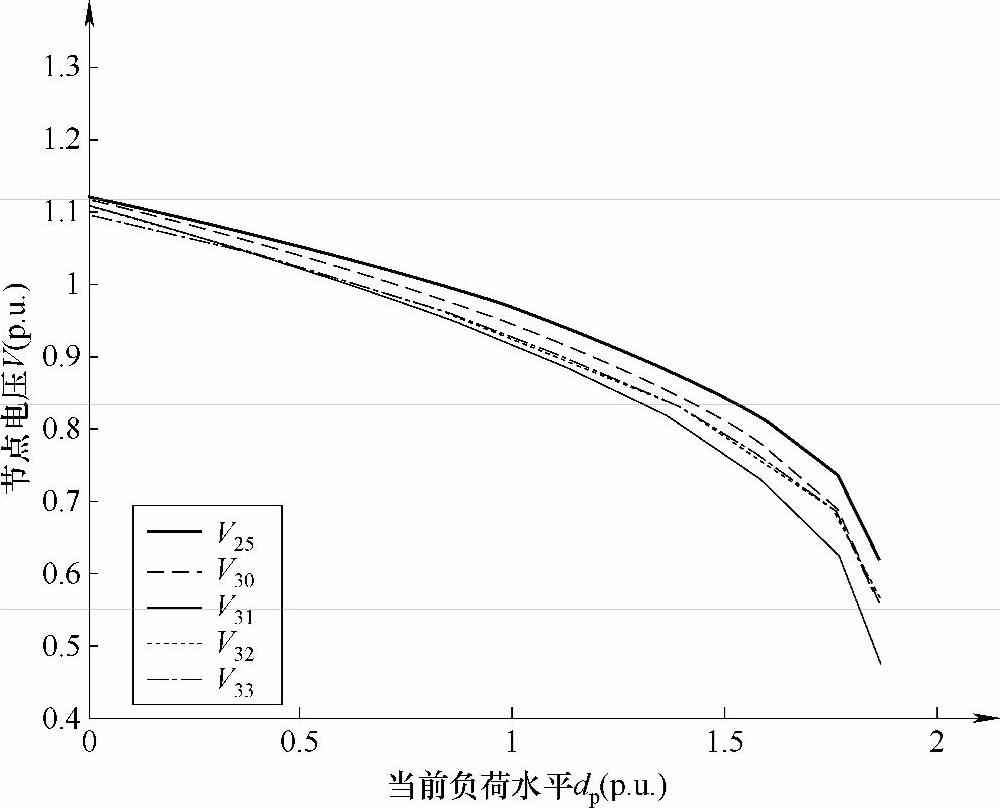
图3-4 IEEE-57节点系统当前负荷水平d_p与负荷节点电压V₂₅、V₃₀、V₃₁、V₃₂和V₃₃的关系

（2）最优潮流仿真结果比较

图3-5分别示出了由单目标最优潮流模型与改进的多目标最优潮流模型在ω₁=1时求得的对应于当前负荷水平的系统最优发电成本。由图中可见，两种优化模型求得的系统最优发电成本相差很小且变化趋势相同，这也验证了本书提出的改进多目标最优潮流模型的正确性。但需要指出，两种优化模型计算采用的节点电压约束为0.90p.u.～1.10p.u。(www.xing528.com)

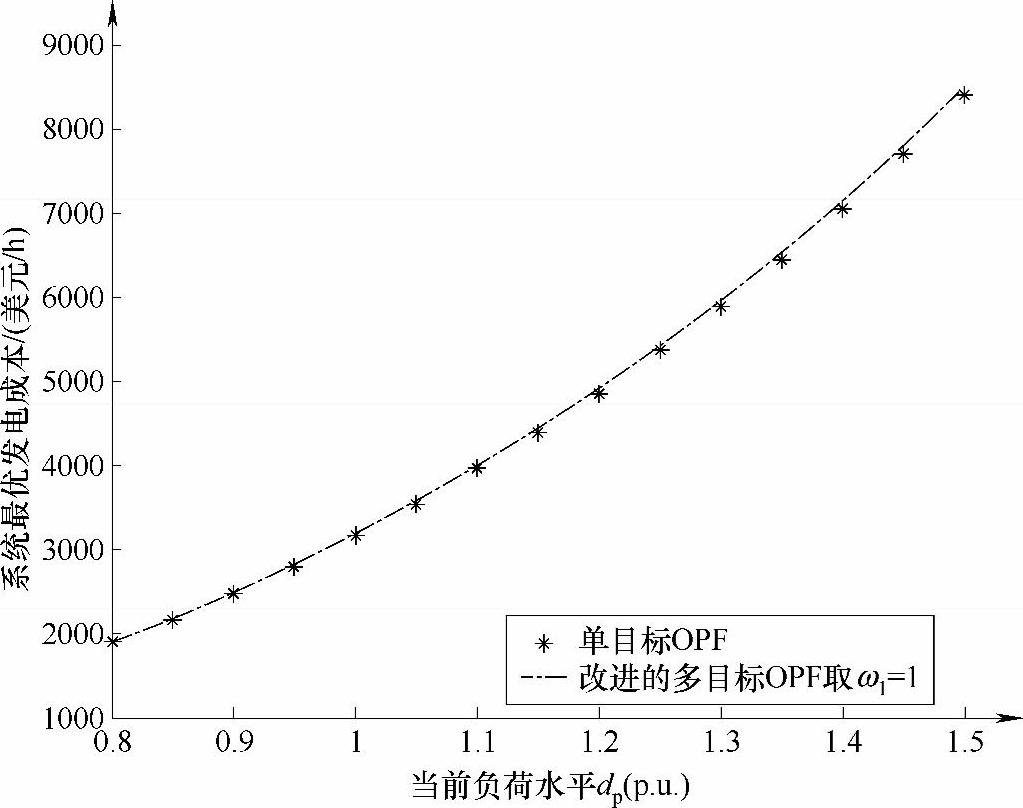
图3-5 两种优化方法求得的对应于不同负荷条件下的IEEE-57节点系统最优发电成本比较（节点电压约束取0.90p.u.～1.10p.u.）

当以测试系统给定的节点电压限制0.94p.u.～1.06p.u.作为约束时，将得到图3-6所示的优化结果。采用以上两种优化模型求解不同负荷条件下的系统最优运行解时，随着系统负荷水平的升高，在d_p＞1.08以后，两种优化方法都遇到了收敛问题，即对于d_p＞1.08的当前负荷水平，在该节点电压约束下不存在最优运行解。

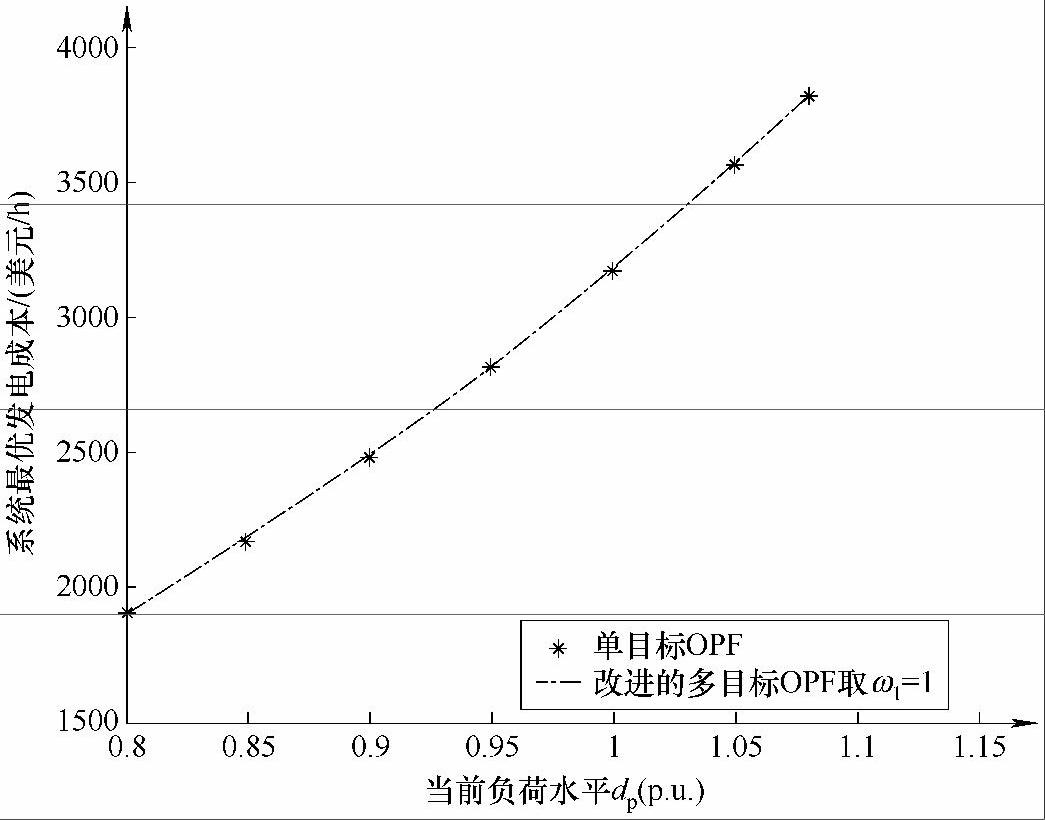
图3-6 两种优化方法求得的对应于不同负荷条件下的IEEE-57节点系统最优发电成本比较（节点电压约束取0.94p.u.～1.06p.u.）

（3）多目标最优潮流优化结果分析

由于电力系统的运行限制如节点电压约束、线路潮流约束等，一般其限值都保留了一定的裕度，为了获得可行解，必要时在容许范围内的稍许越限是允许的，因此，可取节点电压约束为0.90p.u.～1.10p.u.进行优化研究。根据前面的优化结果分析，结合系统电压稳定分析结果，将d_p=1.08对应的负荷水平在考虑发电机无功功率限制时的实际负荷裕度0.1636p.u.作为系统的理想负荷裕度，进行的优化问题计算。

图3-7分别给出了改进模型在不同权重系数取值下优化得到的对应于不同负荷条件下的系统最优发电成本。

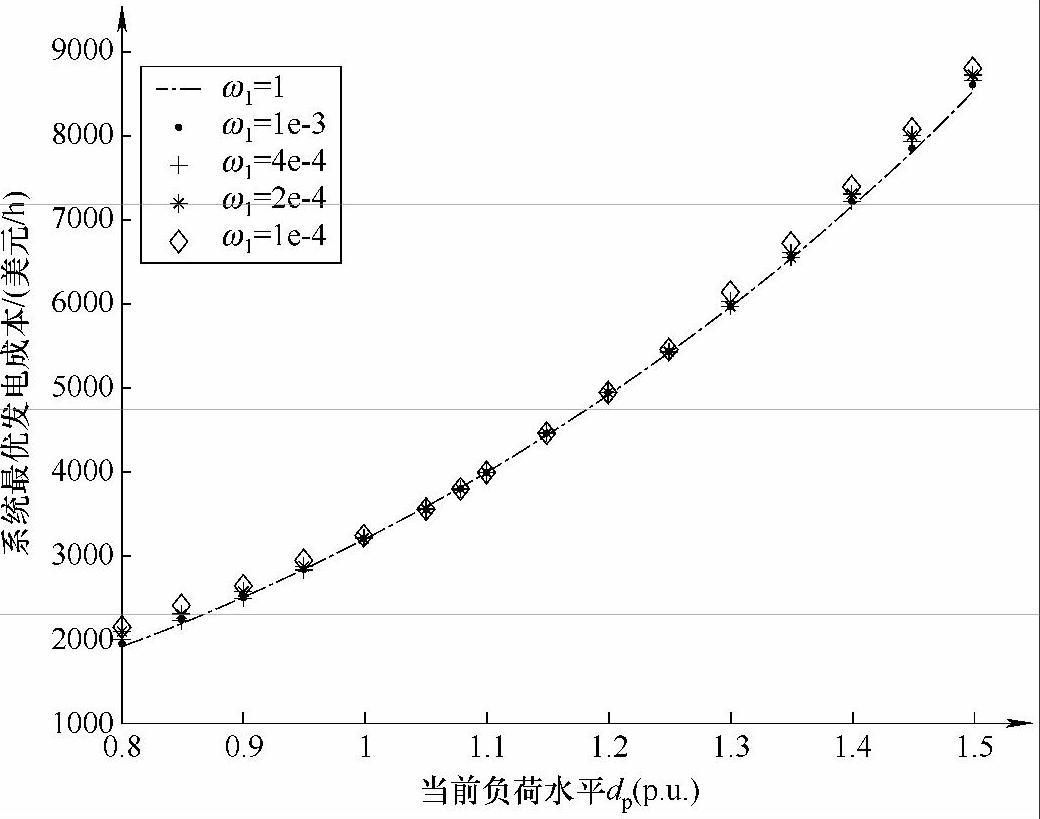
图3-7 改进模型在不同权重系数取值下优化得到的对应于不同负荷条件的最优发电成本（IEEE-57节点系统）

由图3-7可见，当考虑系统电压安全裕度时，目标函数中不同的权重系数所对应的系统最优发电成本不同。其中，对应于同一负荷水平下，考虑电压安全裕度的系统最优发电成本与不考虑电压安全裕度的最优发电成本之差即为系统在该负荷条件下的电压安全成本，如图3-8所示。对应于同一负荷水平下，随着权重系数ω₁逐渐减小，系统的电压安全成本逐渐升高，因此，确定一个合理的权重系数以正确估计系统维持电压安全必须额外付出的经济代价，是现场运行人员需要慎重对待的一个问题。

由图3-8可见，当前负荷水平d_p介于1.00～1.15之间时，随着权重系数的改变，系统的电压安全成本变化不大，但随着系统当前负荷水平偏离d_p=1.08越大，系统的电压安全成本越高。因此，可以根据不同负荷条件下系统的最优发电成本和电压安全成本，确定系统的理想负荷运行点为d_p=1.00～1.15，即该负荷水平下，在保证系统足够电压安全裕度的前提下，系统的最优发电成本与电压安全成本最小，验证了本书提出的改进多目标最优潮流模型的有效性。而且，由该方法获得的系统电压安全成本可以为系统运行人员和市场参与者提供重要的安全、经济信息。

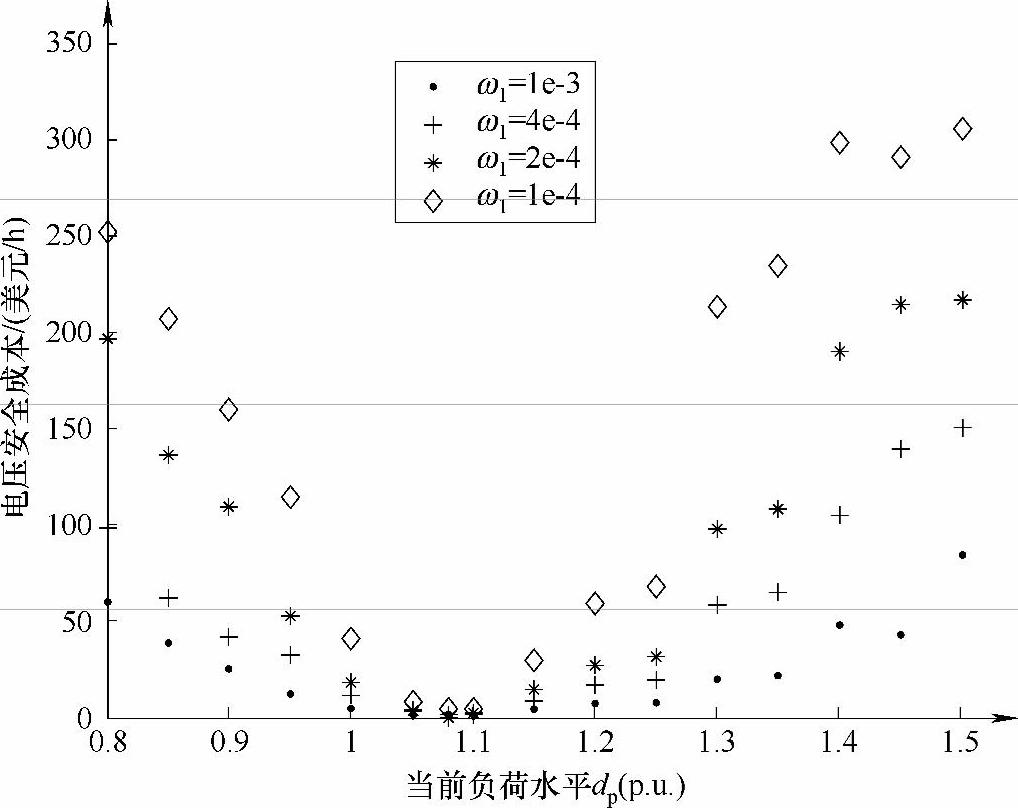
图3-8 改进模型在不同权重系数取值下优化得到的对应于不同负荷条件的系统电压安全成本（IEEE-57节点系统）

本研究优化方法采用的全系统负荷以线性、恒功率因数增长的负荷增长方式虽然比较常用，但用于确定系统的理想负荷裕度则显得比较保守。如图3-3和图3-4所示，两组负荷节点随着其负荷水平的升高，节点电压呈现出明显不同的响应程度，节点25、30、31、32和33的电压反应灵敏，可作为研究的关键区域。本书将在后面的章节中对于这种局部负荷增长对系统电压安全水平的影响进行有针对性的研究。

对于实际的电力系统优化运行分析，运行人员可根据系统网络结构分析、电压稳定分析以及以往运行经验，确定一个比较合理的理想负荷裕度，该理想负荷裕度的确定不必拘泥于整个系统负荷的线性、恒功率因数增长方式，而是根据节点或区域负荷的不同特点，确定一个具有现实意义的理想负荷裕度指标。通过将该指标引入所提出的优化问题模型^[3-8]，对当前负荷条件下的优化计算结果可以为参与系统运营的所有市场主体提供重要的安全、经济信息。