理想负荷裕度指标优化策略

如2.2节所述，表征系统电压安全、稳定的电压稳定指标有很多种，裕度指标的计算涉及过渡过程的模拟和临界点的求取问题，包含的信息量较大，能够考虑到各种限制的发生，因此受到了研究者的广泛关注。在计算电压安全裕度指标时，网络中各负荷节点的功率可以按照任意方式增长，以逼近临界运行点。一般情况下，通用的负荷增长方式可以表示为

式中，λ表示负荷增长参数；D∈R^2l（l为负荷节点数）表示负荷增长的方向向量，前l个元素对应于相应节点的有功负荷增长，后l个元素对应于相应节点的无功负荷增长。只要某一负荷节点的有功/无功功率发生变化，D的相应元素就不是0。通过修改向量D中的适当元素可以形成节点负荷增长、区域负荷增长或全系统负荷增长方式。

假设系统当前运行点的负荷水平用向量A_p（A_p∈R^2l，l为负荷节点数，其元素以MW、Mvar为单位或者是由基准值计算得到的标幺值）表示，对应于该负荷水平的临界运行点的负荷水平用向量A_c（A_c∈R^2l）表示，则电压安全裕度指标可用系统负荷裕度来表征，即

式中，M∈R^2l为向量，其中的每一个元素m_i（i=1，2，…，2l）表示相应节点的有功、无功裕度。为了将该指标引入最优潮流问题模型，以形成考虑电压安全裕度的最优运行问题，通常采用的指标形式为最大负荷距离指标、最小电压安全裕度指标和理想负荷裕度指标。

1.最大负荷距离指标

最大负荷距离指标的含义是使系统的当前运行点与临界点的距离（即系统的电压安全裕度M）最大化。

将该指标计入优化问题模型时，以最大化向量M中最小的元素m_min为目标，可以将m_min作为单一目标函数，在满足系统运行约束条件下，寻求使m_min最大化的系统最优安全运行解；或者将m_min作为优化目标之一，通过加权求和与其他的优化目标形成多目标最优潮流问题。这两种方法的优化问题模型分别为

和

式中，ω₁和ω₂为权重系数，可取ω₁+ω₂=1；g（x_p，u_p，A_p）表示待优化的其他目标函数，可以是系统运行成本或系统有功网损；下标p和c分别用来标识系统的当前运行点和临界运行点；x∈R^N表示系统的状态变量，包括除平衡节点外的所有节点电压相角、非发电机节点电压幅值、PV节点发电机的无功出力和平衡节点发电机的有功与无功出力；u∈R^M表示系统的控制变量，包括PV节点发电机有功出力和端电压幅值、有载调压变压器电压比以及并联补偿装置容量；F（·）=0表示节点潮流方程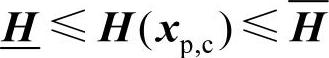；表示线路潮流约束；和分别为H（x_p，c）的上、下限；x和分别为x_p，c的上、下限；和分别为u_p，c的上、下限。

显然，式（3-3）为了最大化系统的电压安全裕度，获得的优化运行策略势必以比较高的运行成本（或比较高的系统有功网损）为代价，丧失了系统运行的经济性。式（3-4）通过加权求和考虑了系统运行的另一个优化目标，如经济性目标，从而在一定程度上实现了最小化系统运行成本（或系统有功网损）与最大化系统电压安全裕度的折中；但由于该方法无法对负荷裕度设定一个定值，从而使得对所确定的权重系数的合理性产生质疑。

2.最小电压安全裕度指标

最小电压安全裕度指标以使向量M中最小的元素m_min大于或等于事先确定的门槛值作为判据，即

m_min≥m_th （3-5）(www.xing528.com)

式中，标量参数m_th表示系统允许的最小电压安全裕度。

采用该指标的优化问题模型为

式中，目标函数G（x_p，u_p，A_p）可以是单目标，也可以是多个子目标的联合。这里将最小电压安全裕度指标作为系统优化运行必须满足的约束条件，因此最小电压安全裕度m_th的取值与该优化问题的最优解有着紧密的联系，事先确定的最小电压安全裕度如果取得过大，将导致优化问题无解。

3.理想负荷裕度指标

理想负荷裕度是针对具体的系统，根据电压稳定分析结果或运行人员的经验确定的系统负荷裕度期望值，可用向量M_g（M_g∈R^2l）表示。

采用目标规划方法将理想负荷裕度指标计入优化问题模型时，虽然可以预先确定各个负荷节点的理想负荷裕度，但为了简化起见，通常可选择系统中几个薄弱节点的理想负荷裕度指标进行优化计算，而且可以定义各个目标的优先级顺序。假定有k个目标（即计及k个薄弱节点的理想负荷裕度指标），n个优先级（n≤k），则基于目标规划的优化问题模型表示如下：

式中，ω₁和ω₂分别为两个优化子目标的权重系数，可取ω₁+ω₂=1；表示待优化的目标函数，可以是系统运行成本或系统有功网损；向量）分别表示系统k个薄弱节点的实际负荷裕度和理想负荷裕度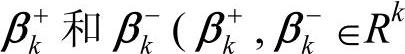；）分别表示与M_k相对应的、与M_kg相比的目标超过值和不足值，即正、负偏差变量向量；p_i（i=1，2，…，n）表示第i个优先级的优先因子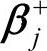；和（j=1，2，…，k）分别为向量和中的第j个元素；和表示在同一优先级p_i中，第j个目标的正、负偏差变量的权重系数。

由式（3-3）、式（3-4）、式（3-6）和式（3-7）比较以上三种指标可以发现，最大负荷距离指标应用简单，不必像最小电压安全裕度指标和理想负荷裕度指标那样，在进行优化计算之前，需要事先确定系统的最小电压安全裕度和理想负荷裕度。但是对于电网结构比较强壮以及电源充裕度比较高的系统来说，当仅将最大化负荷裕度作为系统优化运行的目标函数时，可能会丧失系统运行的经济性，不利于资源的优化配置。

计及最小电压安全裕度指标的优化问题模型，将该指标仅作为约束条件，即寻求满足事先规定的系统最小电压安全裕度的经济运行点，不但有利于维持系统的电压安全裕度，而且在一定程度上实现了系统的经济运行。

最大负荷距离指标与最小电压安全裕度指标在计入优化问题模型时，取的是节点负荷裕度最小的量。实际上，对于某一具体的系统而言，系统的电压稳定与否往往取决于关键发电机节点和薄弱负荷节点的状态。因此，也可以采用系统薄弱节点的负荷裕度作为电压安全裕度指标计入优化问题模型。

理想负荷裕度指标的提出与应用体现了目标规划方法的思想，即给定若干目标以及实现这些目标的优先顺序，在有限的资源条件下，使总的偏离目标值的偏差最小。