自由经济和计划经济的对比分析

内容提要：本节首先通过案例分析了沙普利的延迟接受算法，然后通过TOC制约理论来分析配对算法，指出配对理论是寻求自己和对方的系统产出最大化，由于系统的产出由瓶颈决定，所以双方都是在寻找与自己能力最相近的配对，这样的配对才是稳定的，系统的产出才是最大化的。

创新要点：使用TOC制约理论来分析配对理论，二者的核心均是寻找与自己能力最相近的配对来实现系统产出最大化，这样的配对才是稳定的配对。

计划经济和自由经济的分歧由来已久，经济学家要么支持计划经济，要么支持自由经济。

哈耶克在理论上证明了计划经济不能实现资源的最优配置，并于1974年获得诺贝尔经济学奖。在差不多的时间，里奥尼德·赫维茨证明了市场经济也不能实现资源的最优配置。但是由于西方国家过分相信市场经济的资源配置作用，不愿将诺贝尔经济学奖授予赫维茨。直到2007年爆发金融危机，市场经济为社会发展造成了严重的损失，在实践上证明了赫维茨的市场经济不能实现资源的最优配置的理论是正确且有效的，最终于2007年将诺贝尔经济学奖颁发给了90岁的赫维茨。很遗憾的是，赫维茨在获得诺贝尔经济学奖3个月后去世了。

埃尔文·罗斯在《共享经济：市场设计及其应用》中写到：“绝大多数的市场运行都介于‘亚当·斯密的看不见的手’和‘中央计划经济’之间。市场既不是中央计划经济，因为市场的参与者决定了谁得到什么，又不是完全地自由放任，因为市场参与者都知道市场有其运行规则。”计划经济和自由经济是经济的两种极端情况，现在的市场经济运行于这两个极端之间。这一点和战争理论的兰切斯特法则类同，现实的战斗介于兰切斯特法则的远距离原则和近距离原则的这两个极端之间。

既然计划经济和市场经济均不能实现资源的最优配置，那么有什么方法能实现资源配置呢？诺贝尔经济学奖获得者罗斯开创了一个全新的经济学分支——市场设计，通过市场设计达到资源的最优配置。市场设计通过不断地调整规则，市场能够更好地工作。

罗斯使用盖尔和沙普利创立的“延迟接受算法”应用于肾脏市场，拯救了许多人的生命；应用于“全国住院医生配对程序”，通过这一程序，每年美国约有20000名医生找到了心仪的医院作为自己职业生涯的起点。罗斯还帮助设计了纽约高中配对系统，每年有约9万名高中生通过这一系统择校。由于罗斯和沙普利对“稳定分配理论和市场设计实践”的贡献，两人分享了2012年的诺贝尔经济学奖。

市场设计的核心是配对，罗斯在书中写到：“市场设计的新经济学对配对及其市场进行了科学的阐述，这也是本书所要讨论的内容……配对在经济学术语中可以解释为，我们如何从生活中得到既是我们所选择的，同时也是选择我们的事物。”配对的解决方案为延迟接受算法（deferred-acceptance algorithm），也称为盖尔-沙普利算法（the Gale-Shapley algorithm），简称GS算法。此算法由戴维·盖尔和罗伊德·沙普利所创立，沙普利是博弈论创始巨头之一。这一个算法简单到连初中的学生都能理解，但是它却解决了困扰人类多年的配对难题。

罗斯在《经济共享》中指出了市场设计的四个原则，分别为保持稠密度、避免阻塞、保证安全和简单方便应用。他写到：“每一个市场的成功不仅需要保持市场的稠密度，避免阻塞，保证安全，还需要简单方便使用（注意，不是简单）。”Uber、Airbnb、Facebook、维基百科、嘀嘀打车、Youbube、股权众筹等共享经济市场也具有以上特点。

7.3.9.1　市场设计之延迟接受算法

本章会通过例子介绍延迟接受算法，并且文中有延迟算法的动画链接，可以点击进行练习。

下边将通过约会配对问题对“立即接受算法”和“延迟接受算法”进行讲解。

（1）立即接受算法

对于约会的配对，传统的做法（被称为immediate acceptance，即“立即接受法”），是大家都去追自己最心仪的女生。而这个女生面对几位追求者，要立刻做个决定。被拒绝的男生们调整一下心情，再去追求心中的No.2。以此类推。

这样做法有一个严重的问题：当你被你的No.1拒绝后，再去追求你的No.2的时候，你心中的No.2可能已经在第一轮中选择了其他人。但坑爹的是，有可能你正是你心中No.2心中的No.1，但是她并不知道。所以她在第一轮中，因为没有被你追求，而屈就他人。比及你在第一轮中表白失败，再去找你的No.2时，已然晚矣。

网上有一个简单的例子，假设班上三男（分别是A、B、C）三女（分别是x、y、z），见下图（左女右男）（如图7-65所示）：

他们心中对异性的排名见下图（如图7-66所示）。在女x的心中A＞B，意味着A要好于B。

第一轮中，男生们向心中的No.1女示好，即A、B两男向心中最喜欢的x女示好，而C男向y女示好（如图7-67所示）。

如果采用立即接受算法，此轮之后的结果是，x-A、y-C两对结成情侣。注意，y女虽然心中首选是B男，但是由于B男在此轮中正在追逐x女，无奈下y女屈就于唯一来献殷勤的C男。比及第二轮开始时，唯一还没配对的就是z女和B男了，所以B男只能接受z女（如图7-68所示）。

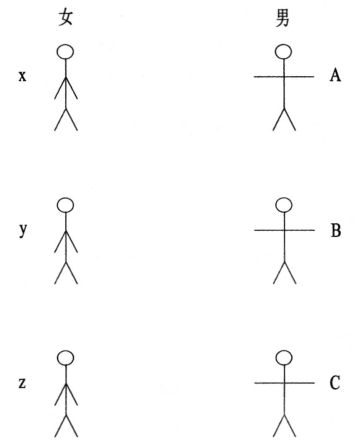
图7-65　待配对的三男三女

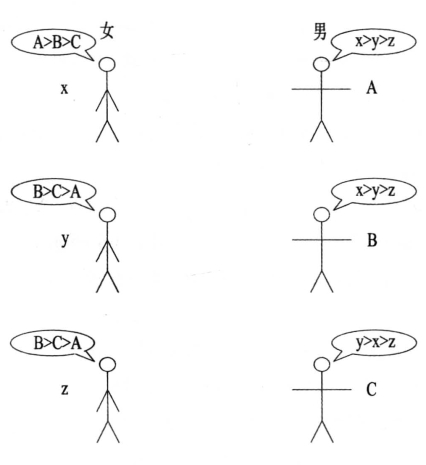
图7-66　心中对异性的排名

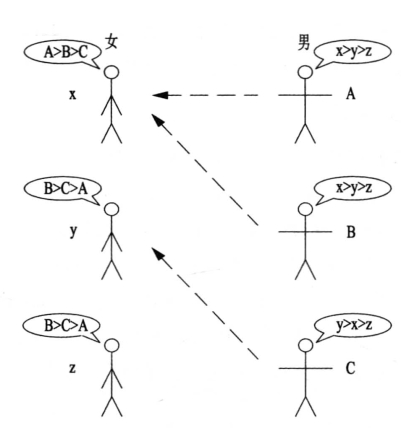
图7-67　第一轮各自向心中的第一号示爱

图7-68　立即接受算法的配对结果《传统配对）

最后的结果是x-A、y-C、z-B三对恋人。注意：y女和B男两人都更愿意离开自己的现任伴侣而彼此在一起。这种不稳定的状态就是很多文学影视作品的来源。在数学上，这也恰恰被称为是“不稳定”的组合。顾名思义，我们希望能够有种算法，给我们的结果是所有配对都是稳定的。

（2）延迟接受算法

延迟接受算法的操作：每个男生在第一轮中向自己心中的No.1示爱。但是各位姑娘们不用立即决定，而是先hold住了。在第二轮中，每个男生再向心中的No.2示爱。从第二轮开始，每位姑娘们只保留自己到现在为止所收获的最心仪的男生（但是不用答应他，只hold在心里），而拒绝其他所有人。而被拒绝的男生（也就是现在尚没有人hold着你的男生）则继续在下一轮中向心中排名的下一个姑娘表白。以此类推，一轮轮继续下去，直到所有想示爱的男生都示完为止。此时，每个手中有offer的姑娘，可以选择接受。

以上就是立即接受算法的做法。大家算一下，就会发现，在我们这个简单的例子中，最后的结果是x-A、y-B、z-C三组恋人终成眷侣。而这是一种稳定的结果。所有六人中，你不可能找到一男一女符合以下条件：他们都更愿意抛弃已有的伴侣而与彼此在一起（如图7-69所示）。

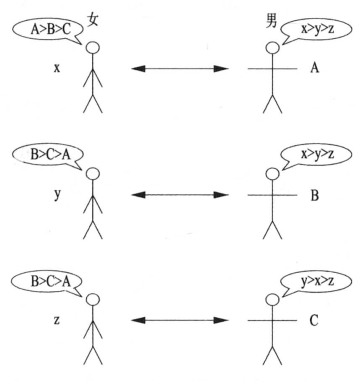
图7-69　延迟接受算法的配对结果

延迟接受算法能够从数学上证明是一定会产生稳定配对的算法。这使它成为一个重要的工具，因为这类的配对问题在现实生活中太常见了。罗斯在《共享经济》中介绍了他将延迟接受算法分别运用于肾脏移植市场，全国住院医生配对市场和高中择校系统，实现了稳定的配对，取得了非常好的成果。

（3）延迟接受算法（盖尔-沙普利算法）的动画使用讲解

1）打开网址：http://mathsite.math.berkeley.edu/smp/smp.html，可以进行延迟接受算法的动画练习，更直观，更容易理解。

其中exhibit walkthrough表示演练，可以点击进去进行演练。Free Experiments表示自由练习。这个算法通过自由练习，几分钟就会明白它的原理。可以点击进入自由练习（如图7-70所示）。

图7-70　

2）右下角显示的4、5、6分别表示配对数量是4对还是5对，可以选择；第二行表示男人选择女人还是女人选择男人；第三行表示快速和逐步的解法；第四行表示开始新的一局练习；第五行表示返回主菜单（如图7-71所示）。(www.xing528.com)

3）默认的是4对配对，男人选择女人。每个人旁边列出了她自己的偏好。比如女a的偏好为B＞C＞D＞A。如果她接到B和C的追求，她会保留B，放弃C，但只是保留，并没有确定，在接到新的追求后，她会再做对比，保留排在前边的，放弃排在后边的（如图7-72所示）。

图7-71　

图7-72　

4）将男A通过鼠标移到她的第一选择女a处，男B移到女C处，男C移到女a处。此时女a面临选择，根据她的排序，她选择男C，放弃男A（如图7-73所示）。

5）点击男A他将回到原处，然后将男A移到他的第二选择女c处。此时女c面临选择。女c按照自己的偏好选择男A，放弃男B（如图7-74所示）。

6）点击男B，他将回到原处。将男B移到他的第二选择女b处（如图7-75所示）。

图7-73　

图7-74　

图7-75　

7）将男D移到自己的第一选择女b处。女b面临选择，她选择保留男B，放弃男D（如图7-76所示）。

8）点击男D，他将回到原处，将男D移到他的第二选择女d处（如图7-77所示）。

此时，所有配对完成，这个配对是稳定的，因为你不可能找到一男一女符合以下条件：他们都更愿意抛弃已有的伴侣而彼此在一起。

下边的配对就是不稳定的配对（如图7-78所示）。

对于男C而言，女d要好于现在的配对女b，所以可能的话，男B希望更改为女d；对于女d而言，男C要好于男B，所以可能的话，女d希望更改为男C。这就存在了一个不稳定，男C希望找到更好的配对女d，并且女d也希望找到更好的配对男C。最后两队配对被拆散，男C与女d完成新的配对。稳定的结果如下图所示（如图7-79所示）。

计划经济和自由经济均不能完全实现资源的有效配置，当市场失灵时，市场设计是可以实现资源的有效配置的一种方式。

图7-76　

图7-77　

图7-78　

图7-79　

配对理论可以通过TOC制约理论进行理解。假设有两个组，1组中包括A、B、C这3个成员，成员的能力分别为100、80和60。2组成员分别为a、b、c这3个成员，能力分别为90、70和50。1组和2组成员进行配对，配成3对。根据TOC制约理论，系统产出的大小由系统的瓶颈大小决定。所以A和a配对时，Aa的系统产出是90，Ca的系统产出60。类似于1组代表电脑的CPU，2组代表电脑的显卡，假设电脑这个系统的性能只由两者的组合决定，则电脑的性能取决于CPU和显卡中性能最差的（如表7-1所示）。

表7-1　TOC制约理论与配对理论

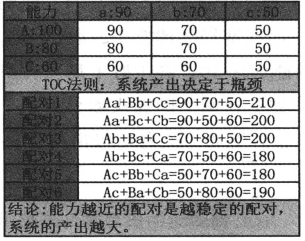
在所有的6种配对组合中，配对1的系统产出最大，为210。并且配对1组合中的每个配对都是与自己能力最相近的一方进行配对。与配对1相比，配对2并不是稳定的配对，Be配对中的B如果选择与b配对，Bb的产出将增加20。同理，Cb中的b如果选择与B配对，Bb的产出将增加20，Be配对中的B和Cb配对中的b均有动力脱离原来的配对形成新的配对Bb，从而整个系统产出从200上升到210。与配对1相比，配对4是更不稳定的配对，因为如果换成配对1，整个系统的产出将增加30，重新配对得到的利益更大。

配对不仅可以是二维的，也可以是三维或者多维的，配对所遵循的原则是相同的。

田忌赛马与配对的关系

罗斯说：“配对在经济学术语中可以解释为，我们如何从生活中得到既是我们所选择的，同时也是选择我们的事物。”那么博弈（田忌赛马）就是选择我想选择，但不是你想选择的事物。如果说配对是一种合作，争取系统的产出最大化，那么博弈就是一种反合作，争取自己的产出最大化。配对时，参与者有相同的目标，博弈时，参与者有独立的目标。

在田忌赛马的博弈中，齐王有上等马、中等马、下等马这三匹马，田忌也有上等马、中等马、下等马这三匹马。两人进行赛马，谁赢的赛局多，谁获得胜利。赛局1，齐王胜3局，齐王获胜；赛局2-5，齐王胜2局，输1局，齐王获胜；赛局6，齐王胜1局，输2局，田忌胜。假设齐王三匹马的能力分别为100、80和60，田忌三匹马的能力分别是90、70和50。两人比的是胜局而不是差距。假设两人比的是三匹马的能力，那么A-a+B-b+C-c=30，即无论田忌如何安排赛局，他的马与齐王的马的差距都是30，他都会失败。而在赛局的博弈中，胜的多和胜的少的问题，齐王上等马比田忌上等马的能力多10，齐王胜1局；齐王上等马比田忌下等马的能力多50，齐王胜1局，这两个胜局从能力差距上相差很大，但是从赛局比分上没有区别，都是胜1局，或者可以说博弈论（田忌赛马）不存在“边际”（如表7-2所示）。

表7-2　TOC博弈论的田忌赛马与配对理论

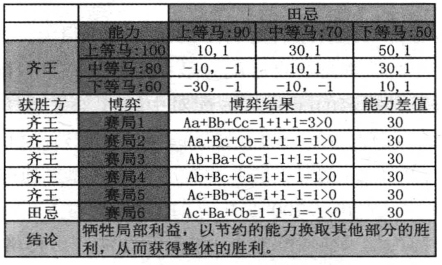
田忌通过改变与齐王赛马的配对，放弃下等马这局比赛，选用上等马对中等马，中等马对下等马这样的节约能力的方式，以2∶1战胜齐王。田忌选择的配对恰不是齐王想要的配对。如果齐王理解了田忌的策略，则齐王会在未来的赛局中极力避免田忌想要的配对。