产品购买数量与价格变化对维持天数的影响分析

对于数量n，是经济学最喜欢分析的因素，因为对于质量为m的某种物品，10个比5个多，3个比4个少，而资源配置是可以通过数量大小来衡量配置的效果。但对于不同质量m的物品，没办法直接比较，比如一本书的质量比一个汉堡大还是小呢？我应该将有限的金钱用来买书还是买汉堡呢？

6.5.1.1　替代品

内容提要：本节通过消费预算和维持天数的限制，给出了替代品的数学函数，并且绘制了替代品的二维图形。给出了三种替代品的数学函数，并且绘制了三种替代品的三维图形。也可以通过金钱的消费速度和维持天数来分析替代品。

创新要点：

1.给出了替代品的数学函数。

2.给出了替代品在各种情况下的二维图形。

3.将替代品扩展到三种，并且给出了各种情况下的三维图形。

设产品A和产品B为互相可以替代的产品，产品A的价格为PA，产品B的价格为PB，时间t天的消费预算为E。如果只消费A产品，每天需要消耗数量为a；如果只消费B产品，每天需要消耗数量为b。设购买A产品的数量为x，则A产品可以维持x/a天；剩下的金钱用于购买B产品可以维持（E-xPA）/（PBb）天。自变量x所代表的购买量不能超过预算E，x的取值范围大于等于0。则可以得到在固定约束下，时间t关于产品A购买量的方程，即有

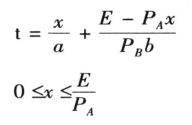
第一个公式可化简为

这个斜率k为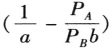的一条线段，当斜率大于0时，这是一条单调增加的线段。即，说明B产品每天消费金钱的数量PBb大于A产品每天消费金钱的数量PAa。A产品的最大购买量为图中的F点，购买量为E/PA，最大的维持天数为E/（PAa），即将全部预算购买A产品可以维持的总天数。线段FG下的阴影部分为可以选择的点。当预算天数为t1时，相交线段FG与A点，如果选择偏好在边界A点上，那么t1天消费x1单位的A产品和（E-PAx1）/PB单位的B产品。如果预算维持天数为t2，t2大于可以维持的最大天数E/（PAa），t2为不可达到的点，可以通过增加消费预算E来弥补（如图6-37所示）。

当斜率k为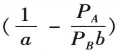小于0时，这是一条单调递减的线段。即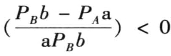，说明B产品每天消费金钱的数量PBb小于A产品每天消费金钱的数量PAa。A产品的最大购买量为图中的L点，购买量为E/PA，最小的维持天数为E/（PAa），即将全部预算购买A产品可以维持的总天数。线段GL下的阴影部分为可以选择的点。

目标维持天数t3交线段GL于C点，此时A产品的购买量为x4，B产品的购买量为（E-PAx4）/PB单位（如图6-38所示）。

当斜率大于0，即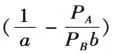大于0时，B产品每天消费金钱的数量PBb大于A产品每天消费金钱的数量PAa。目标维持天数为t1天。当A产品价格为PA1时，偏好点为A点，此时A产品的购买数量为x1。B产品的消费数量为（E-PA1x1）/PB。当A产品的价格从PA1时上升到PA2时，约束线GH相交t1与B点，A产品的购买量从x1上升到x2。这是只有一种替代品的情形，作者在吉芬物品一节中已经详细解释此种情况（如图6-39所示）。

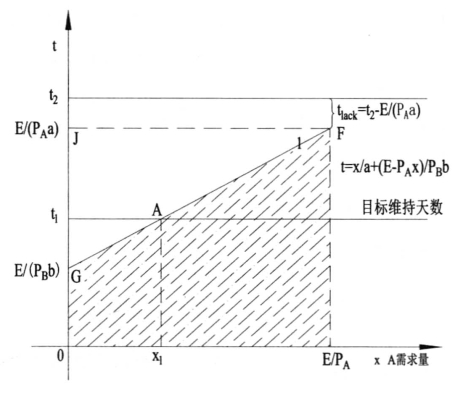
图6-37　替代品分析—斜率大于0时的可取范围

图6-38　替代品分析一斜率小于0时的可取范围

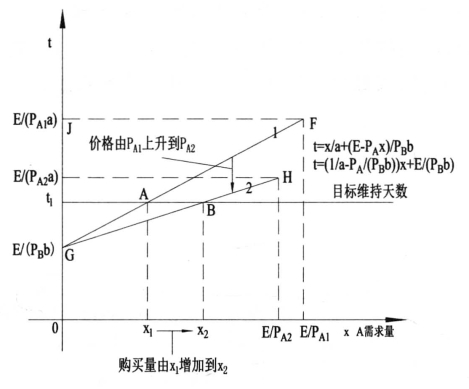
图6-39　替代品分析一斜率大于0时，价格变化的影响

当斜率小于0，即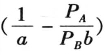小于0时，B产品每天消费金钱的数量PBb小于A产品每天消费金钱的数量PAa。目标维持天数为t3天。当A产品价格为PA4时，偏好点为C点，此时A产品的购买数量为x4。B产品的消费数量为（E-PA4x4）/PB。当A产品的价格从PA4时上升到PA5时，约束线段GN相交t3与D点，A产品的购买量从x4下降到x5（如图6-40所示）。

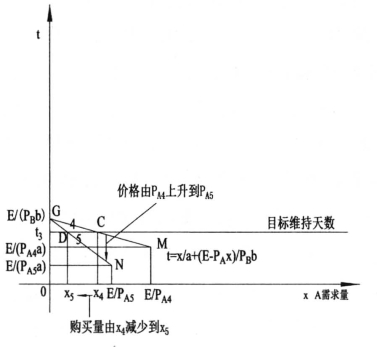
图6-40　替代品分析一斜率小于0时，价格变化的影响

当斜率为0时，即A产品每天金钱消费的速度等于B产品每天金钱消费的速度。如果此时维持的天数为E/（PBb），那么线段GQ为最大约束线段，A和B产品的购买数量可以为满足约束条件下的任意组合（如图6-41所示）。

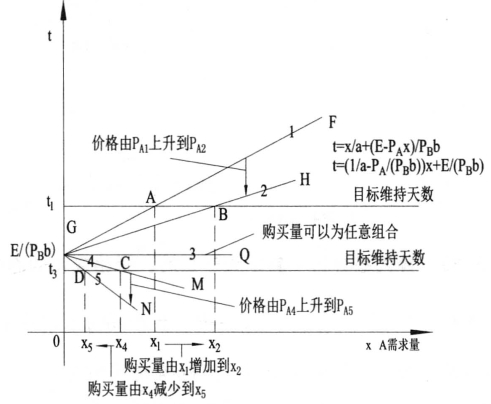
图6-41　图6-39替代品分析一价格变化对购买量的影响

当替代品为三种时，也可以给出类似的函数。

设产品A，产品B和产品C为互相可以替代的产品，产品A的价格为PA，产品B的价格为PB，产品C的价格为PC，时间t天的消费预算为E。如果只消费A产品，每天需要消耗数量为a；如果只消费B产品，每天需要消耗数量为b；如果只消费C产品，每天需要消耗数量为c。设购买A产品的数量为x，则A产品可以维持x/a天；设购买B产品的数量为y，则B产品可以维持y/b天；剩下的金钱用于购买C产品可以维持（E-xPA-yPB）/（cPc）天。自变量x和y所代表的购买量不能超过预算E，x和y的取值范围大于等于0，二者购买量所需金钱不能超过预算E。则可以得到在固定约束下，时间t关于产品A和产品B购买量的方程，即有

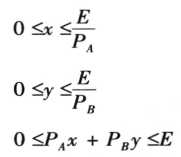
第一个公式可化简为

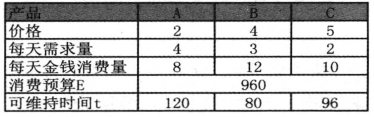
产品A每天消费的金钱为aPA，产品A每天消费的金钱为bPB，产品A每天消费的金钱为cPc。当产品A的价格为2元每个，每天只消费产品A需要4个，每天金钱的消费量为8元；产品B的价格为4元每个，每天只消费产品B需要3个，每天金钱的消费量为12元；当产品C的价格为5元每个，每天只消费产品C需要2个，每天金钱的消费量为10元。当消费预算E为960元，则产品A可以维持120天，产品B可以维持80天，产品C可以维持96天（如表6-33所示）。

表6-33　基于金钱消耗速度的替代品分析(www.xing528.com)

第一个公式简化为

在MATLAB中输入如下命令，可以得到下边的图形（如图6-42所示）。

图6-42　替代品A和B的定义域和值域

图形下边和x正轴及y正轴所包围的图形为维持天数t可以的取值范围，而图形代表了维持天数t的边界。

切换到x-z轴上，可以看到x对应的产品A的取值范围为0-480，对应的梯形为维持天数可以取值的范围0-120。当x取值为480时，即预算的960元完全用来购买产品A，可以维持的天数为120天。由于自变量x的斜率为1/3-2/5＜0，所以随着y的增加，值域t是减少的（如图6-43所示）。

切换到y-z轴上，可以看到y对应的产品B的取值范围为0-240，对应的梯形为维持天数可以取值的范围0-80。当y取值为240时，即预算的960元完全用来购买产品B，可以维持的天数为80天。由于自变量x的斜率为1/4-1/5＞0，所以随着x的增加，值域t是增加的（如图6-44所示）。

画出与z轴垂直的平面，与z轴相交点的值为95。所表达的意思是：当目标维持天数为95天时，三种产品在边界上的最大值分别是多少。

图6-43　替代品A的定义域和值域

图6-44　替代品B的定义域和值域

在MATLAB中输入如下命令，可以得到下边的图形（如图6-45所示）。

图6-45　替代品—目标维持天数为95天

网格平面2等于95与产品A和产品B的值域有一系列的交点，这些交点组成了在目标天数为95天时，产品A、产品B可以取得的值，同时也就决定了产品C可以取得的值。

当产品A的价格从每个2元上升到每个2.2元，维持时间t可以取值的范围变小。

继续在MATLAB中输入如下命令，可以得到产品A变化后的图形为下图的条形曲面（如图6-46所示）。

条形曲面与x正轴及y正轴所包围的体积变小，维持天数t的取值范围在减少。当产品A的价格为2元时，目标维持天数为95天，深灰色边界曲面与网格曲面相交一系列交点，设交点为（x1，y1，95）。交点代表当满足目标维持天数95时，产品A、产品B和产品C可以购买最大量的组合，其中，产品C的购买量通过函数公式可以求得。当产品A的价格从2元上升到2.2元，产生了条形曲面，条形曲面与目标网格曲面有一系列交点，设为（x2，y2，95）。由于产品A的价格上涨，为了达到目标维持天数，可以通过调整一种产品、两种产品或者三种产品的购买量来达到目标维持天数。

图6-46　替代品—目标维持天数为95天，A从2元上升到2.2元

设产品A的金钱消费速度v1元/天，产品B的速度v2元/天，产品C的速度v3元/天，且v1＜v2＜v3。在固定预算S下，金钱消费速度v越小，维持的时间t越长，即t=s/v。

设用于购买产品A的钱数为x，购买产品B的钱数为y，购买产品C的钱数为z，消费预算为s，目标维持天数为t，且所有金钱均被使用购买三种产品。得到如下函数

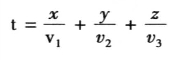
约束为

当目标维持天数t小于金钱消耗最快产品可以维持的天数s/v3，即t＜s/v3，那么三种产品的购买量可以为任意组合，就能满足维持天数，且三者的总的金钱消耗小于预算s，即x+y+z＜s。

当目标维持天数小于产品B可以维持的天数，大于产品C可以维持的天数，即s/v3＜t＜s/v2。当产品A的价格上升时，v1增加从而导致维持天数t减少。可以通过减少产品C的预算z来增加产品A的预算x或者B的预算y来增加天数，从而使维持天数t保持不变。也可以不减少产品C的预算z，通过减少产品B的预算y来增加产品A的预算x，来保证维持天数t不变。

当目标维持天数小于产品A可以维持的天数，大于产品B可以维持的天数，即s/v2＜t＜s/v1。当产品A的价格上升时，v1增加从而导致维持天数t减少。可以通过减少产品C的预算来增加产品A预算x来增加天数。也可以不减少产品C的预算z，通过减少产品B的预算y来增加产品A的预算x，来保证维持天数t不变。如果某产品的维持天数大于目标天数，增加这个产品的预算可以增加维持的天数。如果替代品有多种，均可以通过如上的分析给出替代品的数学函数。