探讨方向α在博弈论中的应用

内容提要：本节给出了博弈论经典案例《囚徒困境》的数学函数和MATLAB图形，指出博弈论不存在边际，使囚徒困境的理解更加直观和简单。使用诺贝尔奖获得者沙普利的配对理论，指出哪种配对是稳定的配对。配对是我们如何从生活中得到既是我们所选择的，同时也是选择我们的事物。而博弈论是选择我想得到的但却是对手不想得到的。博弈论是配对理论的一种反应用。本节不仅分析了博弈双方在自利情况下的稳定配对，还分析了存在自利、克己和利他多种情况下的稳定配对。

创新要点：

1.给出了囚徒困境的数学函数，指出博弈论不存在边际。

2.使用MATLAB绘制了囚徒困境的三维模型，使其更直观，更容易理解。

3.使用配对理论分析了囚徒困境的稳定配对，并且分析了博弈双方分别在利己、克己和利他情况下的稳定配对。

博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。表面上不同的相互作用可能表现出相似的激励结构（incentive structure），所以它们是同一个游戏的特例。其中一个有名有趣的应用例子是囚徒困境。

具有竞争或对抗性质的行为称为博弈行为。在这类行为中，参加斗争或竞争的各方各自具有不同的目标或利益MV。为了达到各自的目标和利益，各方必须考虑对手的各种可能的行动方案α，并力图选取对自己最为有利或最为合理的方案α。比如日常生活中的下棋、打牌等。博弈论就是研究博弈行为中斗争各方是否存在着最合理的行为方案，以及如何找到这个合理的行为方案的数学理论和方法。

6.2.3.1　囚徒困境与配对理论

1950年，由就职于兰德公司的梅里尔·弗勒德（Merrill Flood）和梅尔文·德雷希尔（Melvin Dresher）拟定出相关困境的理论，后来由顾问艾伯特·塔克（Flbert Tucker）以囚徒方式阐述，并命名为“囚徒困境”。经典的囚徒困境如下：

警方逮捕甲、乙两名嫌疑犯，但没有足够证据指控二人有罪。于是警方分开囚禁嫌疑犯，分别和二人见面，并向双方提供以下相同的选择：

若一人认罪并作证检控对方（相关术语称“背叛”对方），而对方保持沉默，此人将即时获释，沉默者将判监10年。

若二人都保持沉默（相关术语称互相“合作”），则二人同样判监半年。

若二人都互相检举（互相“背叛”），则二人同样判监2年。

用表格概述如下（如表6-1所示）：

表6-1　囚徒困境案例

若对方沉默、我背叛会让我获释，所以会选择背叛。

若对方背叛指控我，我也要指控对方才能得到较低的刑期，所以也是会选择背叛。

二人面对的情况一样，所以二人的理性思考都会得出相同的结论——选择背叛。背叛是两种策略之中的支配性策略。因此，这场博弈中唯一可能达到的纳什均衡，就是双方参与者都背叛对方，结果二人同样服刑2年。

这场博弈的纳什均衡，显然不是顾及团体利益的帕累托最优解决方案。以全体利益而言，如果两个参与者都合作保持沉默，两人都只会被判刑半年，总体利益更高，结果也比两人背叛对方、判刑2年的情况较佳。但根据以上假设，二人均为理性的个人，且只追求自己个人利益。均衡状况会是两个囚徒都选择背叛，结果二人判监均比合作为高，总体利益较合作为低。这就是“困境”所在。例子有效地证明了：非零和博弈中，帕累托最优和纳什均衡是互相冲突的。

在博弈论中，是不存在边际的，即可选择的点是不连续的，不可导。我们来构建函数，使博弈论的函数可导。假设甲合作的可能性为x，认罪的可能性为1-x，其中0≤x≤1；设乙合作的可能性为y，认罪的可能性为1-y，其中0≤y≤1。假设x，y大于等于0.5时表示合作，小于0.5时表示认罪，并且二人被判刑的总年限为z。则得到如下分段函数

在MATLAB中输入如下函数，可以得到对应的囚徒困境的三维图形（如图6-21所示）。

图6-21　有边际的囚徒困境

表6-2　囚徒困境的四种情况

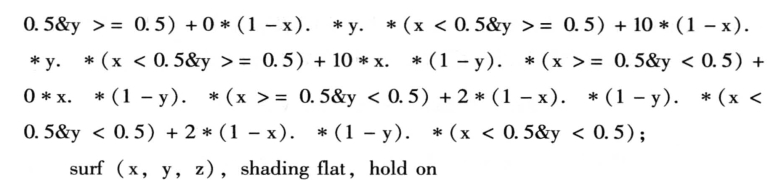
title（′囚徒困境′）

xlabel（x轴　囚徒甲合作）′

ylabel（′y轴　囚徒乙合作）′

zlabel（′z轴　二人总支付）′

当x和y分别合作和认罪时，即当x和y分别等于1，0时，得到三维坐标系内的4个极值点（1，1，1），（1，0，10），（0，1，10）和（0，0，4）。

当x和y分别取0，1时，得到了囚徒困境的四个极值点，构建的函数符合囚徒困境。当甲、乙两人均合作（1，1）时，总的支付为最小的1。但是由于二者均处于自身利益最大化的考虑，二者均选择了认罪（0，0），二者均被判刑2年，二者并没有达到系统的最优值1年，即每人0.5年。

其中甲x对应自己的被判年数的函数为

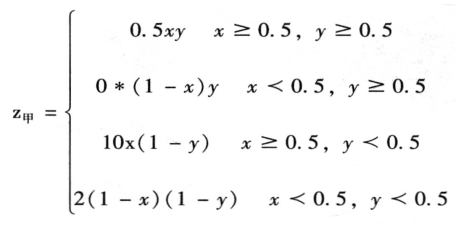
其中乙y对应自己的被判年数的函数为(www.xing528.com)

继续在MATLAB中输入如下程序，得到甲的利益函数。甲利益函数对应的四个极值分别为（1，1，0.5），（0，1，0），（1，0，10）和（1，1，2）（如图6-22所示）。

图6-22　有边际和无边际的囚徒困境

如果限定x和y只能等于0或1，则可以得到无边际的囚徒困境，输入如下程序得到无边际的囚徒困境图形（如图6-23所示）。

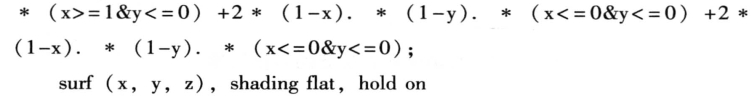
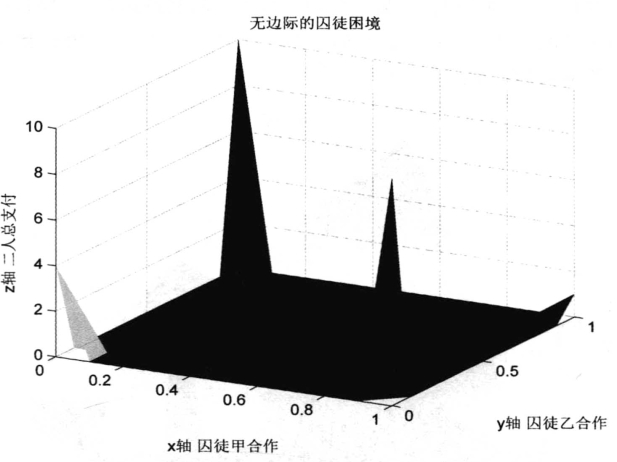
图6-23　无边际的囚徒困境

title（′无边际的囚徒困境′）

xlabel（′x轴　囚徒甲合作′）

ylabel（′y轴　囚徒乙合作′）

zlabel（′z轴　二人总支付）′

在囚徒困境中，一个人的选择不仅影响自己的利益，也会影响对方的利益，而二者处于自己利益最大化的考虑，最终的结果却不是自己的利益最大化。在后边共享经济学中我们会介绍配对理论，此处通过配对理论来解释囚徒困境。

诺贝尔经济学奖获得者埃尔文·罗斯在《共享经济：市场设计及其应用》中写道：“配对在经济学术语中可以解释为，我们如何从生活中得到既是我们所选择的，同时也是选择我们的事物。”而博弈就是选择我们想要选择的，而不让对方选择他们想要选择的。在囚徒困境中，甲和乙均有四种选择，最好的是自己选择认罪，对方选择合作，自己被判0年，对方被判10年；第二种是自己和对方均合作，每人被判0.5年；第三种是双方都认罪，均被判2年；最差的一种是自己合作，对方认罪，自己被判10年，对方释放（如表6-3所示）。

表6-3　囚徒困境的四种配对

在博弈论中推理中，如果对方选择认罪时，自己选择合作会被判10年，而选择认罪会被判2年，所以在对方认罪的前提下，自己选择认罪是最好的策略。当对方选择合作时，如果自己选择合作，会被判0.5年，而选择认罪会被释放，所以在对方选择合作时，自己选择认罪是最好的策略。对方的推理相同，最后两人都选择了认罪，均被判2年。他们的选择没有达到系统的最优值，因为如果二者都选择合作，他们均被判0.5年，比2年少。

在四个配对当中，第一种配对对自己是最有利的，但是对对方是最不利的。当自己选择认罪时，给对方的选择是合作或认罪，而认罪要比合作获得的利益多。这个配对是不稳定的，因为对方会因为自己选择认罪而选择认罪，所以第一种配对达不到自己认罪，对方合作的配对组合。在第一种配对中，不仅为自己选择了最大的利益，也为对方选择了最大的损失。

在第二种配对中，甲不仅为自己选择了合适的利益，也为对方选择了合适的利益。但是这种配对也是不稳定的，对于甲来说，如果对方选择了合作，而自己认罪，自己将获得更大的利益，从而达到第一种配对的状态。但是自己获得的利益是以对方更大的损失换来的，所以总的利益会减少。自己增加的利益为少被判刑2年，而对方的损失是多被判刑8年，自己的自利使两人的配对相比之前多被判刑6年。

第三种配对中，双方都选择了认罪，任何单方面的改变，都不会使自己的境遇变得更好，是一个稳定的配对。如果一方选择合作，那么相应地给对方选择了更好的配对，对方将被释放，而自己的损失增加。在第三种配对中，单方面的改变会变为第一种或第四种配对，都是不稳定的配对。

第四种配对中，自己选择了最大的损失，对方选择了最大的利益，在理智的情况之下，只有利他的精神会导致此种配对的发生。

在囚徒困境的假设中，博弈的双方都是理性利己的，追求自身利益的最大化，而第二种配对则是二人博弈的结果。除了自利，还有两种美德影响着人类的选择。亚当·斯密在《道德情操论》中论述了三种美德，分别为审慎（利己）、合宜（克己）和慈善（利他），而三种美德分别为心理的自爱，同情和理性三种机能推荐给我们。如果博弈双方存在着一方的利他美德，那么第一种或者第四种配对就会发生，利他的一方以对方利益最大化为出发点，自己选择了合作。而如果双方都是利他的话，第二种配对就会发生，均以对方利益最大化为出发点，而达到二人博弈的整体最优点。在存在利他美德的博弈中，第一种，第二种和第四种配对都是稳定的配对。如果博弈中存在克己的情感，即不伤害他人。当对方选择合作时，如果自己选择认罪，将会使对方遭受更大的损失，自己会选择合作；如果对方选择认罪，自己选择合作会使自己遭受更大的损失，所以自己也会选择认罪。如果双方都是克己的，那么第二种配对就是稳定的配对。如果一方是克己的，一方是利己的，那么第三种配对就是稳定的配对（如表6-4所示）。

表6-4　自利、利己和利他情况下的稳定配对

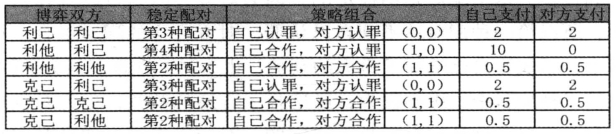
在一个利己的环境中，很难达到个人利益和整体的利益最大化，而在克己或利他的环境中，就可以达到整体的利益和个人的最大化。在哲学部分我们论述过亚当·斯密的哲学。他在《国富论》中论述了自利可以使自己的利益增加，进而使整体的利益增加，而在《道德情操论》论述了审慎（利己）、合宜（克己）和慈善（利他）这三种美德中，推崇克己这种美德。亚当·斯密的完整论述是在遵守克己原则下的利己行为，即不伤害他人的行为，既可以达到个人利益最大化，也可以达到整体利益的最大化。囚徒困境中，博弈二人都选择了坦白，得到了纳什均衡，但不是帕累托最优。二人都选择合作，可以达到帕累托最优。在博弈二人均是利己的假设前提下，只能得到纳什均衡这个次优解，而不能达到帕累托最优解。而在二人均是克己的假设下，可以得到帕累托最优这个稳定的解。这也证明了亚当·斯密在《道德情操论》中推崇克己，而不是自利对整个社会发展是更有利的。

6.2.3.2　科斯定理与博弈论

关于：“非零和博弈中，帕累托最优和纳什均衡是互相冲突的。”不知道这句话是不是博弈论要得到的结论，所以我们尝试以科斯定理的例子加以验证。

以牛吃小麦的案例为例，当牛吃麦子的交易费用为零，均衡点为A点，种麦者与养牛者这个系统所创造的利润为OAFO所包围的面积。

当牛吃麦子有交易费用，假设交易费用固定的话，且交易费用索取权归种麦者，等优曲线还是f1，因为固定的费用会在求导时消除而成为等优曲线f1。所以均衡点与无交易费用时的均衡点是相同的，都是A点，只是种麦者与养牛者这个系统所创造的利润要减少，减少量为固定的交易费用。

当牛吃麦子有交易费用，假设交易费用不固定，交易费用与牛吃麦子的重量成正比p3，且交易费用索取权归种麦者，等优曲线变为fi0，此时均衡点为F点，未达到固定交易费用时的帕累托点A。

如果将均衡点F所需要付出的交易费用作为固定的交易费用，那么均衡点不再是F点，而会达到A点的帕累托最优。所以即使交易费用是相同的，交易费用的衡量方式不同也会影响资源的配置（如图6-24所示）。

在牛吃麦子的例子中，种麦者与养牛者所组成的系统创造的利润要比牛不吃麦子时创造的多，这个系统是不是非零和系统？而在交易费用固定时，是可以达到帕累托最优，在交易费用不固定时，不能达到帕累托最优。

那么博弈论的结论：“非零和博弈中，帕累托最优和纳什均衡是互相冲突的。”是不是就是有错误的？因为在非零和博弈中，交易费用固定时，可以达到帕累托最优。

在战争和企业管理中也存在着很多博弈，比如两家生产相同产品企业的竞争就是博弈，他们通过竞争可能使整个市场扩大，增加了双方的利润，比如可口可乐和百事可乐的竞争增加了可乐市场的总容量，使双方都获益；也可能通过价格竞争都达到利润的最大值，也可能因为彼此竞争降价而进入恶性价格战，导致双方利润减少，甚至破产。

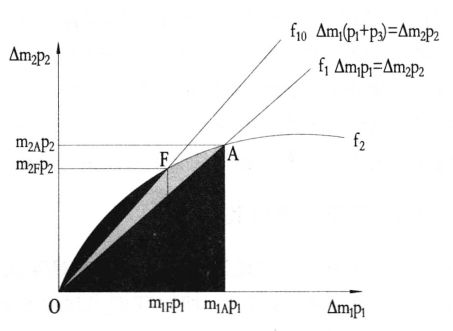
图6-24　交易费用固定和可变对资源配置的影响