成本碗型曲线简介

在战争中，克劳塞维茨说有胜利的顶点；在管理学上有利润曲线和高德拉特所说的浴缸曲线（如图5-23所示）；在经济学上有拉弗曲线和成本曲线；这些曲线都是碗型的，上升和下降沿可能不是对称的。

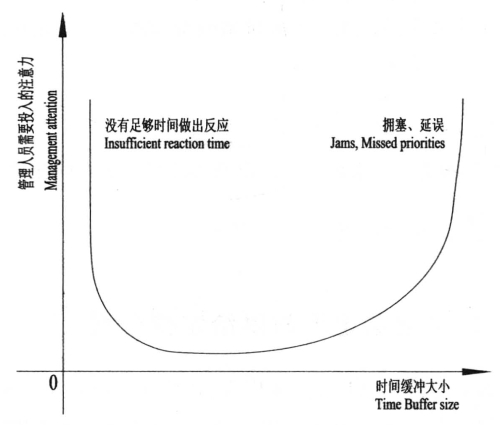
图5-23　碗型曲线

克劳塞维茨在《战争论》中写道：“胜利者不是在每次战争中都能彻底打垮敌人的。胜利常常而且在大多数情况下都有一个顶点。这是大量经验所充分证明了的。于是就发生了如下的情况：大多数统帅宁愿在远离目标的地方停下来，而不愿离目标太近；而有些具有出色的勇敢和高度的进取精神的统帅往往又超过了目标，因而达不到目的。所以只有那些能用少量的手段创建大事业的人才能顺利地达到目的。”

关于成本曲线，肯定会存在一个成本的最低点。刚开始生产某种产品，肯定不能立刻达到成本的最低点，随着管理进步、技能熟练和规模效应等原因，成本在下降，最终达到成本的最低点。此时再增加人力、资本或材料等的投入，边际的利益在下降，成本会增加（如图5-24所示）。

(www.xing528.com)

图5-24　成本碗型曲线

在固定成本C下，供给曲线为S1S1，与纵轴的交点为C。当成本曲线为碗型曲线C1C1时，供给曲线变为S2S2。可以设置成本函数为一个开口向上的抛物线C=a（Q-b）2来表示碗型曲线。供给函数为QS=KS（P-C），由于纵轴为价格，横轴为供给量，为了绘图方便，需要将供给函数进行变换，得到P=QS/KS+C，带入碗型成本曲线，得到新的供给函数为P=QS/KS+a（Q-b）2，绘图得到供给函数图形为S2S2（如图5-25所示）。

成本函数有许多形状，碗型成本曲线只是其中的典型形状之一，对于不同的成本曲线，只要根据供给函数QS=KS（P-C），将成本C替换成对应的成本函数即可。

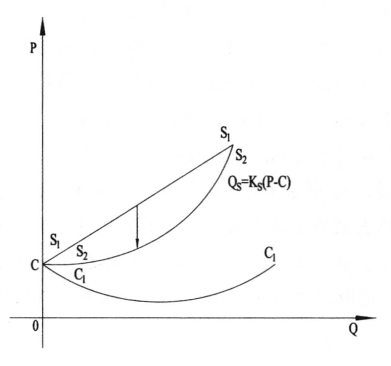
图5-25　成本碗型曲线对供给曲线的影响