需求定律：了解市场需求弹性的重要性

需求弹性是需求定律的一个数学推论，是需求定律的微分形式。需求弹性等于盈余转化率与基础值的乘积。即。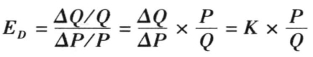

需求的价格弹性（price elasticity of demand），有时称价格弹性（price elasticity），价格弹性为英国新古典派经济学家阿尔弗雷德·马歇尔所创

立。衡量的是：当一种物品的价格发生变动时，该物品需求量相应变动的大小。价格弹性的准确定义是需求量变动的百分比除以价格变动的百分比。即，此公式前有负号，表示价格与需求量负相关。为方便起见，经济学书籍将价格弹性公式前的负号去掉，让所有的弹性都表现为正值，即：

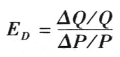
推导过程：

需求定律公式为Q=K（B-P），通过数学对价格P求微分，K也可以看做常数，对应不同的消费者盈余（B-P），K为不同的常数。所以有：

ΔQ=K（B（ΔP）-ΔP），

两边同时除以ΔP，并且乘以，得

对比价格弹性公式，得到

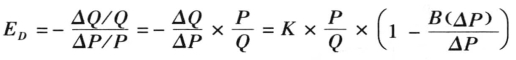
其中B（ΔP）为价格变化对消费者利益的影响，是消费者利益关于价格的函数。

由于对于大多数商品（吉芬物品、奢侈品和投机品除外，价格变化时，此三种产品的消费者利益也发生变化），消费者利益B不随价格改变而改变，在这种情况下，B（ΔP）等于0，所以得到

由于为基础值，是常数，所以需求弹性等于盈余转化率与基础值的乘积。K等于，K为正值。

经济学定义，如果价格变动1个百分点引起的需求量变动超过1个百分点，则该物品就富有需求价格弹性。如果价格变动1个百分点引起的需求量变动不足1个百分点，则该物品就缺乏需求价格弹性。如果价格变动1个百分点引起的需求量变动等于1个百分点，则该物品就拥有单位需求价格弹性。(www.xing528.com)

假设某一物品一直具有单位弹性，价格基值P为100元，此时的需求量Q为200个（假设价格变化对消费者利益B没有影响）。则价格上涨1%，即价格为101元时，需求量也下降1%，即需求量为198个。从而得到。由于假设此物品为单位弹性，所以K值为常数2不变（如图5-6所示）。

带入需求定律公式Q=K（B-P），可得到B=200。所以可以根据不同的价格求得需求量Q=2×（200-P）。

图5-6　需求弹性

从表得到，当基值P=101，Q=198时，价格弹性从1变为0.9802；当基值P=102，Q=196时，价格弹性从0.9802变为0.9608；所以，基值选择不同价格弹性不同（如表5-1所示）。

表5-1　需求弹性

价格不会一直下降，价格以成本为下限；购买量不会一直上升，购买量以总需求为上限。

由于弹性与物理学的弹簧的胡克定律类似，我们来分析两者之间的类同关系（如图5-7所示）。

图5-7　弹簧伸长量与拉力关系

在物理学中，胡克的弹性定律指出：弹簧在发生弹性形变时，弹簧的弹力F和弹簧的伸长量（或压缩量）x成正比，即F=-k·x或ΔF=-k·Δx。k是物质的弹性系数，它只由材料的性质所决定，与其他因素无关。负号表示弹簧所产生的弹力与其伸长（或压缩）的方向相反。其中弹性系数，为因变量增量与自变量增量的比值，这一点与经济学弹性定律的盈余转化率K相同，，K为需求量增量与价格增量的比值。经济学中的需求弹性是一个变化百分比的定义，经济学中增加了基值P/Q，用来表示当前的变化是针对什么价格P和需求量Q的，这一点相当于在胡克定律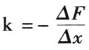左右同时乘以x/F，即同时乘以一个基值，即得到，可以发现此时的公式与需求定律的弹性公式定义完全相同。不同基值类似于选择弹簧测量起点的不同。

弹性系数k和盈余转化率K的大小

在弹簧（或者其他材料）的弹性范围内，弹性系数k不变，为比例系数，当超过此比例范围，弹性系数k值发生改变。需求弹性类同，在某一范围内，盈余转化率K值不变，超过此范围，K值改变（如图5-8所示）。

图5-8　弹簧的胡克定律