资金时间价值及其表现形式

一、资金时间价值的概念

思考一下，今天的100元和几年后的100元，哪一个的价值大一些? 如果我们仅仅是单纯从数字上来看，则很明显它们是一样的。但如果我们考虑一下这100元的增值潜力就会发现，当我将这100元存入银行，几年后我除了拥有100元的本金之外，我还拥有一笔利息，那么我们可以得到，“今天的100元=几年后的100元+利息”; 当我用这100元买卖股票时，还可以获得股利和价差收益，就会得到，“今天的100元=以后的100元+投资收益”。我们不难发现: 今天的100元大于以后的100元。上述例子中的利息、投资收益等都是这100元本金的增值部分，我们将此称为资金的时间价值。

资金的时间价值，是指一定量资金在不同时点上的价值量差额，也称为货币的时间价值。资金的时间价值来源于资金进入社会再生产过程后的价值增值。资金周转使用的时间越长，所获得的利润越多，实现的增值额就越大。资金时间价值的实质，是资金周转使用后的增值额。也就是说不是所有的货币都具有时间价值，只有在循环和周转中的资金，其总量才随着时间的延续按几何级数增长，使得资金具有时间价值。在通常情况下，它相当于没有风险也没有通货膨胀的情况下的社会平均利润率，是利润平均化规律发生作用的结果。

资金的时间价值对于整个企业的财务管理有着极其重要的意义，主要表现在: 其一，便于不同时点上单位货币价值量的比较。不同时点上单位货币的价值不同，因此，不同时间的货币收入不宜直接进行比较，需要把它们换算到相同的时间基础上，才能进行数量比较和比率计算。其二，是正确作出财务决策的前提。资金时间价值是现代财务管理的重要价值基础。它要求合理地节约使用资金，加速资金的周转，以实现更多的资金增值。每个企业在投资某个项目时，至少要取得社会平均资金利润率，否则，不如投资其他的项目或其他的行业。因此，资金的时间价值是评价投资方案的基本标准，在财务决策时，资金时间价值是一项重要的因素。

资金时间价值的大小通常有两种表现形式，一种是绝对数形式即资金时间价值额，即资金在生产经营中带来的真实增值额; 另一种是相对数形式即资金时间价值率。为便于不同数量货币资金之间时间价值大小的比较，在实务中，人们常使用相对数表示资金的时间价值。由于资金价值率经常以利率的形式表示，通常认为它与一般的市场利率相同，实际上资金时间价值率与市场利率是有区别的。市场利率除了包括时间价值因素外，还包括风险价值和通货膨胀因素。但由于资金随时间的增长过程和利息的增长过程在数学上相似，因此，在换算时，应广泛使用计算利息的各种方法。

二、资金时间价值的计算

根据资金具有时间价值的理论，可以将某一时点的资金金额折算为其他时点的金额。因此，掌握资金时间价值的计算就很重要。我们对有关的计算符号进行约定，在以后的学习过程中，某一符号所代表的含义如下:

i为利率(The Discount Rateper Period)，通常指年利率;

I为利息(Interest);

t为计息期间(A Time Period)，如t=5，意味着第五个计息期间;

m为1年中复利的次数，如m=4，意味着按季度计息，一年计息四次;

n为计息期数，如n可以是3年，30个季度，也可以是30个月;

P为现值(Present Value)，又称本金(Present);

F为终值(Future Value)，也称本利和或将来值;

A为每期相等的现金流量(Cash Flow Each Period)，也即年金(Annuity)。

我们一般采用终值和现值两种形式。所谓终值，又称将来值，是现在一定量的资金折算到未来某一时点所对应的金额，即本利和，通常记做F。所谓现值，又称本金，是指未来某一时点上的一定量资金折算到现在所对应的金额，即将来一定量的资金扣除了利息之后的余额，通常记做P。现值和终值是一定量的资金在前后两个不同时点上对应的价值，其差额即为资金的时间价值。终值和现值的计算涉及利息计算方法的选择，目前有两种利息计算方法: 单利计算和复利计算。

(一)单利终值和现值的计算

单利是计算利息的一种方法。在单利制下，只对本金计算利息，所生利息不再计入本金重复计算利息。单利的计算包括计算单利利息、单利终值和单利现值。单利终值，是指本金和未来利息之和。单利现值，是指未来收到或付出资金按单利计算的现在价值。

【例2-1】小陈将1000元存入银行，年利率为10%，求3年后的终值。

解: 利息=本金×年利率×计息期

3年后的利息=1000×10%×3=300(元)

3年后的终值=1000+300=1300(元)

由此，我们可以得到单利终值的一般计算公式为:

F=P+I=P+P×i×n=P(1+i×n)

其中: F为终值; P为现值; I为利息; i为利息率; n为计息期。

(1+i×n)为单利终值系数。

将上述公式进行一个变形，我们就可以得到单利现值的计算公式，即为:

P=F－I=F/(1+i×n)

其中: 1/(1+i×n)为单利现值系数。

【例2-2】小陈希望在3年后从银行取得1000元的本利和，银行年利率为5%，请问他现在要存多少资金到银行?

解: P=F/(1+i×n) =1000/(1+5%×3)≈869.57(元)

从例题可以发现，单利的终值和现值互为逆运算，单利终值系数和单利现值系数互为倒数。

(二)复利终值和现值的计算

复利是计算利息的另一种方法，是指每经过一个计息期，要将该期所派生的利息加入本金再计算利息，逐期滚动计算，俗称“利滚利”。复利的计算包括复利终值、复利现值和复利利息。这里所说的计息期，是指相邻两次计息的间隔，如年、月、日等。除非特别说明，计息期一般为一年。复利终值是按复利计息方式，经过若干个计息期后包括本金和利息在内的未来价值。复利现值是指未来一定时期的资金按复利计算的现在价值，或者说是为取得将来一定的本利和在现在需要投入的本金量，是复利终值的逆运算，也叫贴现。

【例2-3】周全在银行存入3年定期存款1000元，复利年利率为2%，求3年后的终值。

解: 1年后的终值=1000(本金) +1000(本金) ×2%(利率)=1000×(1+2%)=1020(元)

2年后的终值=1020+1020×2%=1020×(1+2%) =1040.4(元)

3年后的终值=1040.4+1040.4×2%=1040.4×(1+2%) =1061.208(元)

注意: 从第2年开始，计息的基础是一个变量，它是前一年的终值，我们可以将3年后的终值的公式进行一个分解: 3年后的终值=1040.4×(1+2%)

↓

1020×(1+2%)

↓

1000×(1+2%)

即3年后的终值=1000×(1+2%) ×(1+2%) ×(1+2%)

=1000×(1+2%)3

由此，我们可以得到复利终值的一般计算公式为:

F=P(1+i)n

其中: (1+i)n为复利终值系数或1元的复利终值，记做(F/P，i，n); 例如， (F/P，2%，3)表示利息率为2%，计息期为3年的1元的复利终值。为了便于计算，我们编制了“1元的复利终值表”(见附表一)。该表的第一行是利息率i，第一列为计息期数n，横纵交叉处即为相对应的复利终值系数。通过该表可查出(F/P，2%，3) =1.0612，即当资金时间价值为2%的情况下，现在的1元和3年后的1.0612元在经济价值上是相等的。在上例中，我们很容易得出1000元3年后的终值=1000×1.0612=1061.2元(与例中结果的误差源于复利终值表中对小数的保留位数)。我们根据该系数表可以将现在的货币资金量换算成将来的货币资金量。该表的作用不仅在于当已知i和n时查找出相对应的复利终值系数值，而且还可用于当已知复利终值系数值和n时查找i，或者当已知复利终值系数值和i时查找n。

【例2-4】周全打算将10000元投资于一个项目，这个项目要使得周全在3年后收回的资金是投资金额的2倍，那么为达到这一目的，他所选择的项目的报酬率最低应是多少?

解:　F=10000×2=20000(元)

20000=10000×(1+i)3

(1+i)3=2

(F/P，i，3) =2

查找“复利终值系数表”，在n=3的横行中寻找2，最接近2的对应i=26%，即(F/P，26%，3)≈2

所以i=26%，即当投资项目的最低报酬率为26%时，才能使现在的资金在3年后达到现值的2倍。

【例2-5】周全打算将10000元投资于一项报酬率为10%的项目，那么要经过多少年才能使现在的资金增加1倍?

解:　F=10000×2=20000(元)

20000=10000×(1+10%)n

(1+10%)n=2

(F/P，10%，n) =2

查找“复利终值系数表”，其最接近的系数值为1.9487

(F/P，10%，7) =1.9487≈2

所以，n=7

即7年后才能使现在的资金增加1倍。

我们将复利终值的计算公式进行一个变形，就得到了复利现值的计算公式，即为

P=F/(1+i)n=F(1+i)－n

其中: (1+i)－n为复利现值系数或1元的复利现值，记做(P/F，i，n); 例如， (P/F，2%，3)表示利息率为2%，计息期为3年的1元的复利现值。同样为了计算的方便，我们编制了“1元的复利现值表”(见附表二)。该表的使用方法与“1元的复利终值表”的使用方法相同。

【例2-6】周全为了3年后能从银行取出1000元，在复利年利率为2%的情况下，当前应存入的金额是多少?

解: P=F(1+i)－n=1000×(1+2%)－3=1000×0.942(查表得) =9420(元)

通过上述计算，我们发现，复利的终值和现值也互为逆运算，复利终值系数和复利现值系数也互为倒数。

(三)年金终值和现值的计算

年金是指一定时期内，每隔相同的时间，收入或支出相同金额的系列款项，通常记做A。在经济领域中，分期付款赊购、分期偿还贷款、融资租赁、养老金的发放、固定资产按照直线法计提的年折旧额、养老保险金、零存整取或整存零取储蓄等都采取年金的形式。

年金按每次收付款发生的时点不同，可分为普通年金、即付年金、递延年金和永续年金。

1. 普通年金

普通年金又称后付年金，是指发生在每期期末的等额收付款项，在现实经济生活中这种年金最为常见，在不加说明时，年金即指普通年金。其计算包括终值和现值计算。

(1)普通年金终值的计算。普通年金终值犹如零存整取的本利和，它是一定时期内每期期末等额收付款项的复利终值之和，记做FA。

根据其定义，我们可知:

年金A，1年的终值=A

年金A，2年的终值=A(1+i)

年金A，3年的终值=A(1+i)2

……

年金A，n年的终值=A(1+i)n－1

所以n期的年金终值为(www.xing528.com)

FA=A+A(1+i)+A(1+i)2+…+A(1+i)n－1　①

将两边同时乘以(1+i)得:

FA(1+i)=A(1+i)+A(1+i)2+A(1+i)3+…+A(1+i)n　②

②－①得:　FA·i=A(1+i)n－A

式中:是普通年金1元在利率为i时经过n期的年金终值，即普通年金终值系数，记做(F/A，i，n)。年金终值系数可以通过查“年金终值系数表”(见附表三)获得。该表的第一行表示利率i，第一列是计息期数n，相应的年金终值系数为其纵横交叉之处。通过查表可以获得(F/A，7%，5) =5.7507(元)。也就是说，每年末收付1元，按年利率为7%计算，到第5年末，期末年金终值为5.7507元。

年金终值的计算公式中有四个变量FA，A，i，n，在我们已经知道i和n的情况下，如果知道FA和A中的任何一个，即可求出另外一个。

因此，普通年金终值的计算公式可简记为:

FA=A·(F/A，i，n)

【例2-7】周全计划在今后5年内每年年末存1000元到银行，年利率为2%。在第5年末，该笔存款的终值为多少?

解: FA=A·(F/A，i，n)

=1000·(F/A，2%，5)

=1000×5.2040

=5204(元)

(2)普通年金现值的计算。普通年金现值是指每期期末等额系列收付款项的复利现值之和，记做PA。

根据其定义，我们可知n期的年金现值为:

PA=A(1+i)－1+A(1+i)－2+…+A(1+i)－n　①

将两边同时乘以(1+i)得:

PA(1+i)=A+A(1+i)－1+A(1+i)－2+…+A(1+i)－(n－1)　②

②－①得: PA·i=A－A(1+i)－n

式中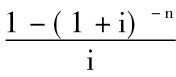，表示1元普通年金在利率为i，期限为n的情况下的年金现值系数，即普通年金现值系数，记做(P/A，I，n)。年金现值系数可以通过查“年金现值系数表”(见附表四)获得。该表的第一行表示利率i，第一列是计息期数n，相应的年金现值系数在其纵横交叉之处。通过查表可以获得(P/A，14%，5) =3.4331。也就是说，每年末收付1元，经过5年，按年利率为14%计算，相当于现值3.4331元。

年金现值的计算公式中有四个变量Pn，A，i，n，在我们已经知道i和n的情况下，如果知道Pn和A中的任何一个，则可求出另一个。

因此，普通年金现值的计算公式可简记为:

PA=A·(P/A，i，n)

【例2-8】周全投资了一个项目，每年年末可得收益10000元，按年利率6%计算，求5年收益的现值。

解: PA=A·(P/A，i，n)

=10000·(P/A，6%，5)

=10000×4.2124

=42124(元)

2. 即付年金

即付年金又称先付年金或预付年金，是指发生在每期期初的等额收付款项。即付年金与普通年金相比，区别就在于收付款的时间不同。

(1)即付年金终值的计算。预付年金终值是指每期期初等额收付款项的复利终值之和。

根据其定义，我们可知n期即付年金与n期普通年金的付款次数相同，只是付款的时间不同，n期即付年金终值比n期普通年金终值多计算一期利息。因此，在n期普通年金终值的基础上乘以(1+i)就是n期即付年金的终值。其计算公式为:

【例2-9】周全计划在今后5年内每年初存1000元到银行，年利率为2%。在第5年末，该笔存款的终值为多少?

解: FA=A·［(F/A，i，n+1) －1］

=1000×［(F/A，2%，6) －1］

=1000×(6.3081－1)

=5308.1(元)

(2)即付年金现值的计算。预付年金现值是指每期期初等额收付款项的复利现值之和。

如前所述，n期即付年金与n期普通年金的期限相同，但由于其付款的时间不同， n期即付年金比n期普通年金少折现一期。因此，在n期普通年金现值的基础上乘以(1+i)，便可求出n期即付年金的现值。其计算公式为:

【例2-10】周全采用分期付款方式购入商品房一套，每年年初付款20000元，分10年付清。若银行利率为5%，该项分期付款相当于一次现金支付的购买价格是多少?

解: PA=A·［(F/A，i，n－1) +1］

=20000×［(F/A，5%，9) +1］

=20000×［7.1078+1］

=162156(元)

3. 递延年金

递延年金是等额系列收付款项发生在第一期以后的年金，即最初若干期没有收付款项，后面若干期每期期末有等额的系列收付款项。它是普通年金的特殊形式，凡不是从第一期开始的普通年金都是递延年金。没有收付款项的若干期称为递延期。

(1)递延年金终值的计算。只要将一共收到或支付n期的年金折算到期末，即可得到递延年金终值。递延年金终值的大小，与递延期无关，只与年金共收到或支付了多少期有关，它的计算方法与普通年金相同。即其计算公式为:

FA=A·(F/A，i，n)

要注意的是，“n”表示的是A的个数，与递延期无关。

【例2-11】周全投资了一个项目，估计从第3年开始到第8年，每年年末可得收益10000元，假设年利率为5%，求投资项目年收益的终值。

解: FA=A·(F/A，i，n)

=10000×(F/A，5%，6)

=10000×6.8019

=68019(元)

(2)递延年金现值的计算。可用三种方法来计算:

方法一: 把递延年金视为n期的普通年金，求出年金在递延期期末m点的现值，再将m点的现值调整到第一期期初。其计算公式为:

PA=A·(P/A，i，n) ×(P/F，i，m)

式中，m为递延期数，n为连续收支期数。

方法二: 先假设递延期也发生收支，则变成一个(m+n)期的普通年金，算出(m+n)期的年金现值，在扣除并未发生年金收支的m期递延期的年金现值，即可求得递延年金的现值。其计算公式为:

PA=A·［(P/A，i，m+n) －(P/A，i，m)］

方法三: 先计算出递延年金的终值，再将终值折算到第一期期初，即可求得递延年金的现值。其计算公式为:

PA=A·(F/A，i，n) ×(P/F，i，m+n)

【例2-12】周全年初在银行存入一笔资金，打算存满3年后，从第4年年末开始连续3年每年年末从银行提取10000元，若银行存款年利率为10%，则他年初要存入多少才能实现计划?

解: 方法一: PA=A·(P/A，i，n) ×(P/F，i，m)

=10000×(P/A，10%，3) ×(P/F，10%，3)

=10000×2.4869×0.7513

=18684.0797(元)

方法二: PA=A·［(P/A，i，m+n) －(P/A，i，m)］

=10000×［(P/A，10%，6) －(P/A，10%，3)］

=10000×(4.3553－2.4869)

=18684(元)

方法三: PA=A·(F/A，i，n) ×(P/F，i，m+n)

=10000×(F/A，10%，3) ×(P/F，10%，6)

=10000×3.3100×0.5645

=18684.95(元)

以上三种方法都可以计算出来，结果反映出来的误差是因小数点的尾数造成的。

4. 永续年金

永续年金是指从第一期期末开始，无限期地在每期期末都有等额的收付款项，如优先股的股利。它是普通年金的一种特殊形式。由于永续年金的期限趋于无限，没有终止时间，因而也没有终值，只有现值。即永续年金现值的计算可以等同为无限期的普通年金现值的计算:

其中: 当n→∞时，(1+i)－n→0

所以，永续年金限制的计算公式为: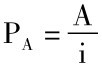

【例2-13】某企业要建立一项永久性帮困基金，计划每年拿出50000元帮助失学儿童，假设年利率为5%，那么现在要筹集多少资金?