如何选择最优方案：基于灵敏度分析的思考

通常,在决策模型中,自然状态的概率和损益值可通过估计或预测得到,不可能十分准确,此外,实际情况也在不断地变化。因此,分析决策所用的数据在多大范围内变动,还能保持原最优决策方案继续有效,称为灵敏度分析。

有两个事件,收益情况如表12-29所示,下面推导转折概率的计算公式:

设p为出现事件E1的概率,(1－p)为出现事件E2的概率。当这两个方案的期望值相等时,即p×a11＋(1－p)×a12＝p×a21＋(1－p)×a22,p值可推导,表示为:

表12-29

若这些数据在某允许的范围内变动,而最优方案保持不变,这个方案就是比较稳定的。反之,若这些数据在某允许的范围内稍加变动,则最优方案就有变化,这个方案就是不稳定的,由此可以得出哪些是非常敏感的变量,哪些是不太敏感的变量,以及在最优方案不变的条件下,这些变量允许变化的范围。

【例12-11】假设有外表完全相同的木盒100只,将其分为两组:一组内装白球,有70盒,另一组内装黑球,有30盒。现从这100盒中任取一盒,请你猜,如这一盒内装的是白球,猜对了得500分,猜错了罚150分;如这一盒内装的是黑球,猜对了得1 000分,猜错了罚200分。有关数据如表12-30所示。

表12-30

试求:

①为使期望得分最多,应选哪一个方案?(www.xing528.com)

②转折概率是多少?

解:

①先画出决策树,如图12-9所示,计算各方案的期望值。

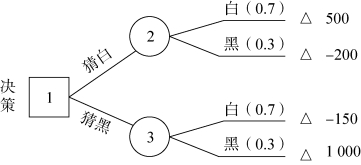
图12-9

猜白方案的期望值为0．7×500＋0．3×(－200)＝290;

猜黑方案的期望值为0．7×(－150)＋0．3×1 000＝195;

经比较,可知猜白方案是最优方案。

②转折概率。

设p为出现白球的概率,(1－p)为出现黑球的概率。当这两个方案的期望值相等时,即

p×500＋(1－p)×(－200)＝p×(－150)＋(1－p)×1 000

求得转折概率p＝0．648 6。即当p＞0．648 6,猜白方案是最优方案;当p＜0．648 6,猜黑方案是最优方案。