决策树：序列决策的有力工具

有些决策问题,当进行决策后又会产生一些新情况,并需要进行新的决策,接着又有一些新情况,又需要进行新的决策。这样决策、情况、决策……就构成一个序列,这就是序列决策。描述序列决策的有力工具之一是决策树。

决策树方法是用树形图表示决策问题,用树的分枝表示各种事件发生的可能,以最大期望值为标准进行剪枝来做决策的一种方法。决策树是由决策点、事件点及结果构成的树形图。决策准则为最大收益期望值、最大效用期望值等。

【例12-8】某石油钻探队在一片估计能出油的荒田钻探。可以先做地震试验,然后决定钻井与否。或不做地震试验,只凭经验决定钻井与否。做地震试验的费用每次3 000元,钻井费用10 000元。若钻井后出油,钻探队可收入40 000元,若不出油,就没有任何收入。各种情况下估计出油的概率已估计出并标在图12-2上。问钻探队的决策者如何做出决策,才能使收入的期望值为最大?

解:

第一步,画决策树。决策树如图12-2所示。

图12-2

第二步,计算各事件点的收入期望值:

将收入期望值标在相应的各事件点处,这时可将原决策树图12-2简化为图12-3。

第三步,按最大收入期望值决策准则在图12-3上给出各决策点的抉择。

图12-3

在决策点[2],max[(34 000－10 000),0]＝24 000,所对应的策略为应选策略,即钻井。

在决策点[3],max[(4 000－10 000),0]＝0,所对应的策略为应选策略,即不钻井。

在决策点[4],max[(22 000－10 000),0]＝12 000,所对应的策略为应选策略,即钻井。

在决策树上保留各决策点的应选方案,把淘汰策略去掉,得到图12-4。

图12-4

第四步,计算事件点(1)的收入期望值,24 000×0．60＋0×0．40＝14 400。

第五步,决策点[1]有两个方案:

①做地震试验,收入期望值为(14 400－3 000);

②不做地震试验,收入期望值为12 000。

max[(14 400－3 000),12 000]＝12 000

结论:12 000所对应的策略为应选策略,即不做地震试验。

这个决策问题的决策序列是,选择不做地震试验,直接判断钻井,收入期望值为12 000元。

【例12-9】设决策者的效用曲线如图12-5所示。试以最大效用期望值为决策准则,对【例12-8】进行决策。

图12-5(www.xing528.com)

解:

采用决策树为工具,在决策树的右端标上纯收入,纯收入＝收入－支出。然后由决策者的效用曲线查得各纯收入相应的效用值,并将此值记在相应的纯收入旁,如图12-6所示。

图12-6

计算事件点(2)、(3)、(4)的效用期望值分别为0．833,0．098,0．672,并标在相应各事件点旁,然后在各决策点[2]、[3]、[4]进行选择,其计算如下:

max2(0．833,0．60)＝0．833;max3(0．098,0．60)＝0．60;max4(0．672,0．68)＝0．68

接着计算事件点(1)的效用期望值为0．739 8,记在事件点(1)旁,决策点[1]的选择为max(0．739 8,0．68)＝0．739 8

根据以上计算,在决策树上可见决策序列是,先做地震试验,若结果好,则钻井;若结果不好,则不钻井。决策分析过程如图12-7所示。

图12-7

【例12-10】某公司需要建工厂来生产一种新产品,新产品的市场寿命为10年,建大工厂的投资费用为280万元,建小工厂的投资费用为140万元,10年内销售状况如下:高需求量的可能性是0．5,中需求量的可能性是0．3,低需求量的可能性是0．2。公司进行了成本—产量—利润分析,在工厂规模和市场容量的组合下,它们的条件收益如下:

大工厂,需求高,每年获利100万元;

大工厂,需求中等,每年获利60万元;

大工厂,需求低,由于开工不足,引起亏损20万元;

小工厂,需求高,每年获利25万元(供不应求引起的销售损失较大);

小工厂,需求中等,每年获利45万元;

小工厂,需求低,每年获利55万元(因工厂规模与市场容量配合得较好)。

要求:

①画出决策树。

②回答该公司应选择哪种方案,可获得最大利润?(用1,2,3,…顺序表示决策点和事件点)

解:

决策树如图12-8所示。

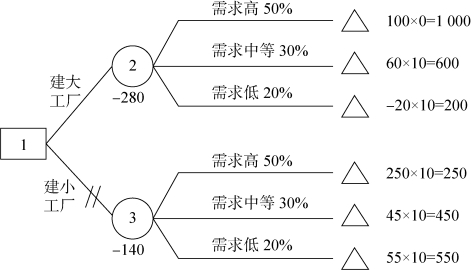
图12-8

E(2)＝1 000×0．5＋600×0．3－200×0．2＝500＋180－40＝640(万元)

E(3)＝250×0．5＋450×0．3＋550×0．2＝125＋135＋110＝370(万元)

按照最大收入期望值决策准则在图12-8上给出决策点1的抉择。在决策点1,按

max[(640－280),(370－140)]＝max[360,230]＝360(万元)

所对应的策略为应选策略,即建大工厂。把淘汰策略去掉。