应用贝叶斯公式修正概率的方法

前面曾提到决策者常常碰到的问题是没有掌握充分的信息,于是决策者通过调查及做试验等途径去获得更多、更确切的信息,以便掌握各事件发生的概率,这可以利用贝叶斯公式来实现,它体现了最大限度地利用现有信息,并加以连续观察和重新估计,其步骤如下:

①先由过去的经验或专家估计获得将发生事件的事前(先验)概率。

②根据调查或试验计算得到条件概率,利用贝叶斯公式:

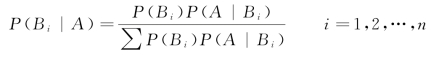
计算出各事件的事后(后验)概率。

【例12-7】某钻探大队在某地区进行石油勘探,主观估计该地区有油的概率为P(O)＝0．5;无油的概率为P(D)＝0．5。为了提高钻探的效果,先做地震试验。根据积累的资料得知,凡有油地区,做试验结果好的概率为P(F|O)＝0．9;做试验结果不好的概率为P(U|O)＝0．1。凡无油地区,做试验结果好的概率为P(F|D)＝0．2;做试验结果不好的概率为P(U|D)＝0．8。问在该地区做试验后,有油与无油的概率各是多少?

解:

先计算做地震试验好与不好的概率。做地震试验好的概率:

P(F)＝P(O)·P(F|O)＋P(D)·P(F|D)＝0．5×0．9＋0．5×0．2＝0．55

做地震试验不好的概率:

P(U)＝P(O)·P(U|O)＋P(D)·P(U|D)＝0．5×0．8＋0．5×0．1＝0．45

利用贝叶斯公式计算各事件的事后(后验)概率。(www.xing528.com)

做地震试验好的条件下有油的概率:

做地震试验好的条件下无油的概率:

做地震试验不好的条件下有油的概率:

做地震试验不好的条件下无油的概率:

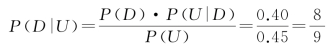
以上计算可在图12-1上进行。

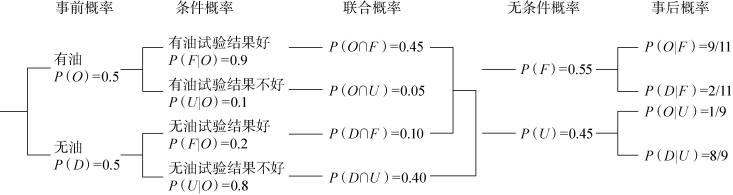
图12-1