如何做出不确定性决策

不确定型决策是指决策者对环境一无所知,这时决策者是根据自己的主观倾向进行决策。因为决策者的主观态度不同,决策准则可分为五种:悲观主义决策准则、乐观主义决策准则、等可能性决策准则、最小机会损失决策准则、折中主义决策准则。

①策略集合:决策者可选的行动方案。记作{Si},i＝1,2,…,m。

②事件集合:可能发生的情况。记作{Ej},j＝1,2,…,n。

③损益函数:每个“策略—事件”对都可以计算出相应的收益值或损失值,记作aij。损益值aij是Si和Ej的函数,即aij＝v(Si,Ej)。

损益值构成的矩阵叫作损益矩阵,损益矩阵

策略集合、事件集合和损益函数组成了决策系统。

【例12-1】设某工厂是按批生产某产品并按批销售,每件产品的成本为30元,批发价格为每件35元。若每月生产的产品当月销售不完,则每件损失1元。工厂每投产一批是10件,最大月生产能力是40件,决策者可选择的生产方案为0件、10件、20件、30件、40件五种。经工厂有关人员分析,断定将发生五种销售情况,即销量为0件、10件、20件、30件、40件。问决策者如何应用五种决策准则进行决策?

解:

决策者可选的行动方案有五种,这是他的策略集合,记作{Si},i＝1,2,…,5。经工厂有关人员分析,断定将发生五种销售情况,即销量为0件、10件、20件、30件、40件,但不知它们发生的概率。这就是事件集合,记作{Ej},j＝1,2,…,5。每个“策略—事件”对都计算出相应的收益值或损失值。如当选择月产量为20件时,销售量为10件,这时收益额为10×(35－30)－1×(20－10)＝40(元)。

可以一一计算出各“策略—事件”对所对应的收益值或损失值,记作aij。将这些数据汇总在矩阵中,如表12-2所示。

表12-2

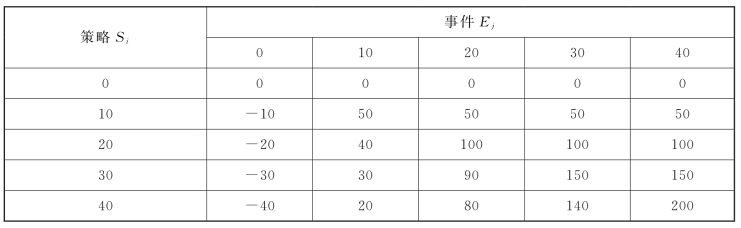
这就是决策矩阵。根据决策矩阵中各元素所代表的含义不同,可称为收益矩阵、损失矩阵、风险矩阵、后悔值矩阵等。

下面讨论决策者是如何应用决策准则进行决策的。

(1)悲观主义(max min)决策准则。

悲观主义决策准则亦称保守主义决策准则,指当决策者面临各事件的发生概率不清时,决策者考虑可能由于决策错误而造成重大经济损失。由于自己的经济实力比较脆弱,他在处理问题时就较谨慎。他分析各种最坏的可能结果,从中选择最好者,以它对应的策略为决策策略,用符号表示为max min决策准则。在收益矩阵中先从各策略所对应的可能发生的“策略—事件”对的结果中选出最小值,将它们列于表的最右列。再从此列的数值中选出最大者,以它对应的策略为决策者应选的决策策略。

如表12-3所示,根据悲观主义决策准则,有max(0,－10,－20,－30,－40)＝0。它对应的策略为S1,即为决策者应选的策略,在这里是“什么也不生产”。上述计算用公式表示为:

表12-3

(2)乐观主义(max max)决策准则。

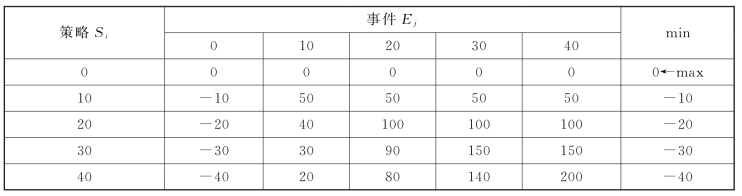
持乐观主义(max max)决策准则的决策者对待风险的态度与悲观主义者不同,当他面临情况不明的策略问题时,他绝不放弃任何一个可获得最好结果的机会,以争取好中之好的乐观态度来选择他的决策策略。决策者在收益矩阵中从各策略所对应的“策略—事件”对的结果中选出最大者,记在表的最右列。再从该列数值中选择最大者,以它对应的策略为决策策略。

如表12-4所示,根据乐观主义决策准则,有max(0,50,100,150,200)＝200,它对应的策略为S5,用公式表示为:

表12-4

(3)等可能性(Laplace)决策准则。

等可能性(Laplace)决策准则是19世纪的数学家Laplace提出的。他认为,当一个人面临着某事件集合时,在没有什么确切理由来说明这一事件比那一事件有更多发生机会时,只能认为各事件发生的机会是均等的。即每一事件发生的概率都是1/事件数。决策者计算各策略的收益期望值,然后在所有这些期望值中选择最大者,以它对应的策略为决策策略。

等可能性决策准则用公式表示为:

如表12-5所示,p＝1/5,期望值为:

即max{E(Si)}＝max{0,38,64,78,80}＝80,它对应的策略S5为决策策略。

表12-5

(4)最小机会损失决策准则。

最小机会损失决策准则亦称最小遗憾值决策准则或Savage决策准则。首先将收益矩阵中各元素变换为每一“策略—事件”对的机会损失值(遗憾值、后悔值)。其含义是,当某一事件发生后,由于决策者没有选用收益最大的策略而形成的损失值。若发生k事件,各策略的收益为aik,i＝1,2,…,5,其中最大者为:

这时各策略的机会损失值为:

(www.xing528.com)

计算结果如表12-6所示。

表12-6

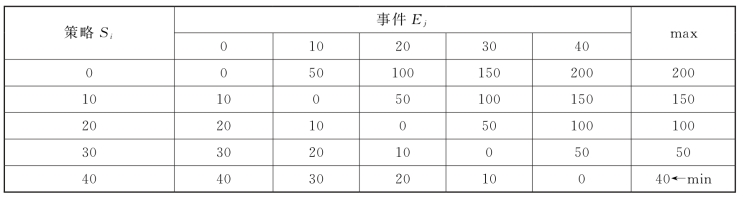
从所有最大机会损失值中选取最小者,它对应的策略为决策策略。用公式表示为:

决策策略为:

min(200,150,100,50,40)＝40→S5。

(5)折中主义决策准则。

当用悲观主义决策准则或乐观主义决策准则来处理问题时,有的决策者认为这样太极端了,于是提出把这两种决策准则综合起来,令α为乐观系数,且0≤α≤1。并用以下关系式表示:

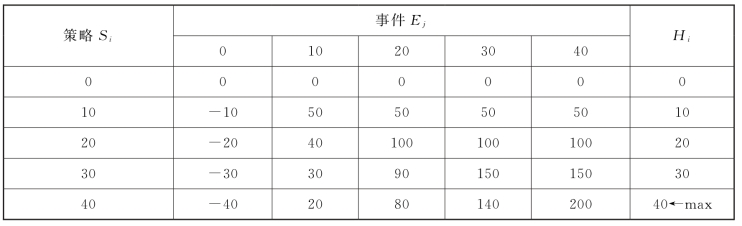
在这里,aimax,aimin分别表示第i个策略可能得到的最大收益值与最小收益值。设α＝1/3,将计算得到的Hi值记在表12-7的右端。

然后选择

决策策略为:

表12-7

【例12-2】设某决策问题的决策收益表如表12-8所示,分别采用悲观主义决策准则、乐观主义决策准则、折中主义决策准则、等可能性决策准则、最小机会损失决策准则进行决策。

表12-8

解:

①采用悲观主义决策准则进行决策,如表12-9所示。

表12-9

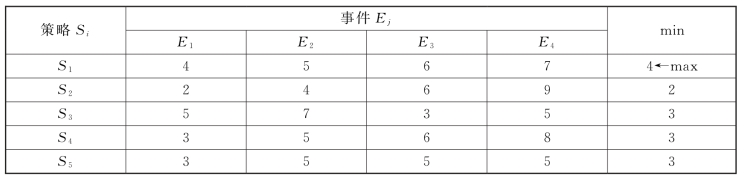
②采用乐观主义决策准则进行决策,如表12-10所示。

表12-10

③采用折中主义决策准则进行决策,如表12-11所示。

表12-11

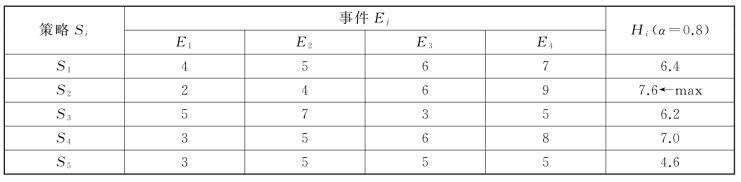
④采用等可能性决策准则进行决策,如表12-12所示。

表12-12

将前面的结果合并,如表12-13所示。

表12-13

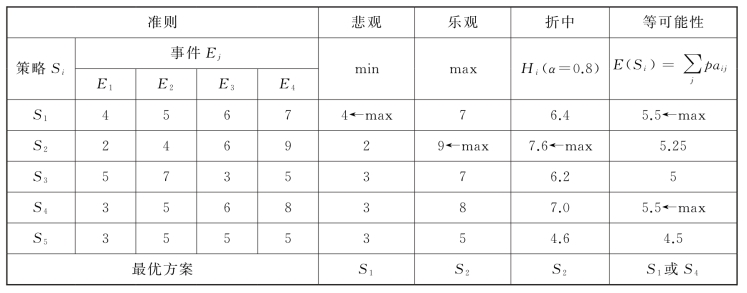
⑤采用最小机会损失决策准则进行决策,如表12-14所示。

表12-14

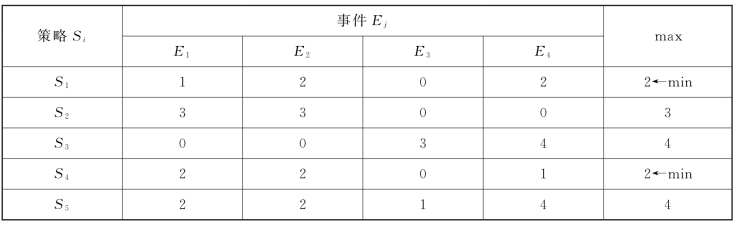
用最小机会损失决策准则决策,最优策略为S1或S4。