矩阵对策解法介绍

矩阵对策的解法有公式法、图解法、线性方程组方法和线性规划方法等。

(1)2×2对策的公式法。

设矩阵对策中

如果A有鞍点,则很快可求出各局中人的最优纯策略;如果A没有鞍点,则可证明各局中人最优混合策略中的均大于0。

于是,由定理6可知,为求最优混合策略,可先求出下列等式组:

当矩阵A不存在鞍点时,可以证明上面等式组(Ⅰ)和等式组(Ⅱ)一定有严格非负解x∗＝,其中,

(2)2×n或m×2对策的图解法。

该方法适用于赢得矩阵为2×n或m×2的对策,也可以用于3×n或m×3的对策,但是对于m和n均大于3的矩阵对策就不适用了。

(3)线性方程组方法。

根据定理4,求解矩阵对策解(x∗,y∗)的问题等价于求解不等式组(11-1)和(11-2),又根据定理5和定理6,如果假设最优策略中的均不为零,即可将上述两个不等式组的求解问题转化成求解下面两个方程组的问题:

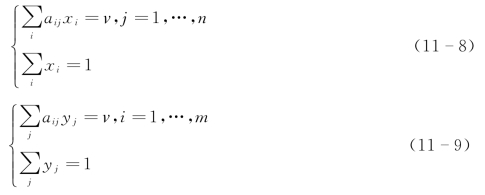
(4)线性规划方法。

由定理5可知,任一矩阵对策G＝{S1,S2;A}的求解均等价于一对互为对偶的线性规划问题,而定理4表明,对策G的解x∗和y∗等价于下面两个不等式组的解。

其中,

是对策的值VG。

定理11:设矩阵对策G＝{S1,S2;A}的值为VG,则:

【例11-6】用公式法求解矩阵对策G＝{S1,S2;A},其中,求它的解及值。

解:

A没有鞍点,由通解式(11-3)－通解式(11-7)计算得到最优解为x∗＝(1/2,1/2)T,y∗＝(1/4,3/4)T,对策值为VG＝5/2。(www.xing528.com)

【例11-7】用图解法求解矩阵对策S2＝{β1,β2,β3}。

解:

显然该问题无鞍点解。

设局中人Ⅰ的混合策略为(x,1－x)T,x∈[0,1]。过数轴上坐标为(0,0)和(1,0)的两点分别作两条垂线Ⅰ－Ⅰ和Ⅱ－Ⅱ,垂线上点的纵坐标值分别表示局中人Ⅰ采取纯策略α1和α2时,局中人Ⅱ采取各纯策略时的赢得值。如图11-1所示。当局中人Ⅰ选择每一策略(x,1－x)T时,他的最少可能的收入为由局中人Ⅱ选择β1,β2,β3时所确定的三条直线:2x＋7(1－x)＝V;3x＋5(1－x)＝V;11x＋2(1－x)＝V。

图11-1

在x处的纵坐标中之最小者,即如折线B1 B B2B3所示。所以对局中人Ⅰ来说,他的最优选择就是确定x,使他的收入尽可能地多,从图11-1可知,按最小最大原则,应选择x＝OA,而AB即为对策值。为求出点x和对策值VG,可联立过B点的两条线段β2和β3所确定的方程:

解得x＝3/11,VG＝49/11。所以,局中人Ⅰ的最优策略为x∗＝(3/11,8/11)T。此外,从图11-1还可以看出,局中人Ⅱ的最优混合策略只由β2和β3组成。

事实上,若记为局中人Ⅱ的最优混合策略,则有:

E(x∗,2)＝E(x∗,3)＝VG

根据定理6可知,必有

根据定理6,可由

求得所以局中人Ⅱ的最优混合策略为y∗＝(0,9/11,2/11)T。

【例11-8】用图解法求解矩阵对策G＝{S1,S2;A},其中S1＝{α1,α2,α3},S2＝{β1,β2},

解:

设局中人Ⅱ的混合策略为(y,1－y)T,由图11-2可知,直线α1,α2,α3在任一点y∈[0,1]处的纵坐标分别是局中人Ⅱ采取混合策略(y,1－y)T时的支付。根据在最不利当中选取最有利的原则,局中人Ⅱ的最优选择就是确定y,以使三个纵坐标值中的最大值尽可能小。从图11-2可见,应选择OA1≤y≤OA2,且对策的值为6,由方程:

图11-2

2y＋7(1－y)＝6和11y＋2(1－y)＝6

求得OA1＝1/5,OA2＝4/9。故局中人Ⅱ的最优混合策略是y∗＝(y,1－y)T,其中1/5≤y≤4/9,而局中人Ⅰ的最优策略只能是x∗＝(0,1,0)T,即取纯策略α2。