矩阵对策的纯策略优化方法

对于一般矩阵对策,有如下定义:

定义:设G＝{S1,S2;A}为矩阵对策。其中:

若等式

成立,记VG＝ai∗j∗,则称VG是对策G的值,称使上式成立的纯局势(αi∗,βj∗)为G在纯策略下的解,αi∗与βj∗分别称为局中人Ⅰ,Ⅱ的最优纯策略。

由定义可知,在矩阵对策中两个局中人都采取最优纯策略(如果最优纯策略存在)才是理智的行为。

【例11-1】设矩阵对策G＝{S1,S2;A},其中,S1＝{α1,α2,α3,α4},S2＝{β1,β2,β3},局中人Ⅰ的赢得矩阵为,求解该矩阵对策。

解:

根据矩阵A,得到表11-1。

表11-1

续表

于是

G的解为(α2,β2),α2和β2分别是局中人Ⅰ和Ⅱ的最优纯策略。

【例11-2】已知矩阵对策G＝{S1,S2;A},其中,S1＝{α1,α2,α3,α4},S2＝{β1,β2,β3,β4},而且局中人Ⅰ的赢得矩阵为求矩阵对策G的解和值。(www.xing528.com)

解:

根据矩阵A,得到表11-2。

表11-2

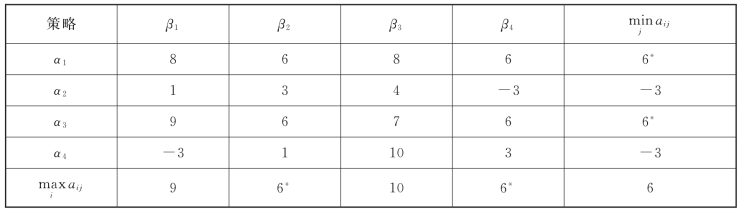
于是(α3,β2),(α3,β4)四个局势都是对策的解,且VG＝6。由例11-2可知,一般矩阵对策的解可以是不唯一的。当解不唯一时,解之间的关系就具有下面两条性质。

性质1 无差别性。即若(αi1,βj1)和(αi2,βj2)是对策G的两个解,则ai1j1＝ai2j2。

性质2 可交换性。即若(αi1,βj1)和(αi2,βj2)是对策G的两个解,则(αi1,βj2)和(αi2,βj1)也是解。

【例11-3】某单位采购员在秋天时要决定冬天取暖用煤的采购量。已知在正常的冬季气温条件下需要用煤15吨,在较暖和较冷气温条件下需要用煤10吨和20吨。假定冬季的煤价随着天气寒冷的程度而变化,在较暖、正常、较冷气温条件下每吨煤价分别为100元、150元和200元。又设秋季时每吨煤价为100元。在没有关于当年冬季准确气象预报的条件下,问秋季应购多少吨煤,能使总支出最少?

解:

这个问题可以看成是一个对策问题,把采购员当作局中人Ⅰ,他有三个策略,在秋天时买10吨、15吨和20吨煤,分别记作策略α1、策略α2和策略α3。

把大自然看作局中人Ⅱ,大自然的“选择”是冬天的气温,也有三种策略,出现较暖的、正常的和较冷的冬天,分别记作策略β1、策略β2和策略β3。

现把该单位冬天取暖用煤全部费用(秋季购煤费用＋冬天不够时再补购煤费用)作为采购员的赢得,采购员的赢得情况如表11-3所示。

表11-3

故对策的解为(α3,β3),即秋季存储煤20吨最为合理。对策G的值VG＝－2 000。