最优服务台数的M/M/c模型优化

仅讨论标准的M/M/c模型,且在稳态情形下,这时单位时间全部费用(服务成本与等待费用之和)的期望值。

其中c是服务台数;c′s是每个服务台单位时间的成本;cw为每个顾客在系统中停留单位时间的费用;L是系统中顾客平均数Ls或队列中等待的顾客平均数Lq(它们都随c值的不同而不同)。因为c′s和cw是给定的,唯一可能变动的是服务台数c,所以z是c的函数z(c),现在是求最优解c∗使z(c∗)为最小。

因为c只取整数值,z(c)不是连续变量的函数,所以不能用经典的微分法。我们采用边际分析法(Marginal Analysis),根据z(c∗)是最小的特点,有:

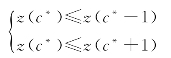
得:

依次求c＝1,2,3,…时L的值,并作两相邻的L值之差,因c′s/cw是已知数,根据这个数落在哪个不等式的区间就可定出c∗。

【例10-11】某检验中心为各工厂服务,要求做检验的工厂(顾客)的到来服从泊松流,平均到达率λ为每天48次,每次来检验由于停工等原因损失为6元。服务(做检验)时间服从负指数分布,平均服务率μ为每天25次,每设置1个检验员服务成本(工资及设备损耗)为每天4元。其他条件适合标准的M/M/c模型,问应设几个检验员(及设备)才能使总费用的期望值为最小?(www.xing528.com)

解:c′s＝4元/检验员,cw＝6元/次,λ＝48,μ＝25,λ/μ＝1．92。

设检验员数为c,令c依次为1,2,3,4,5,求出Ls。计算过程如表10-6所示。

表10-6

将Ls值代入式(10-57)得表10-7。

表10-7

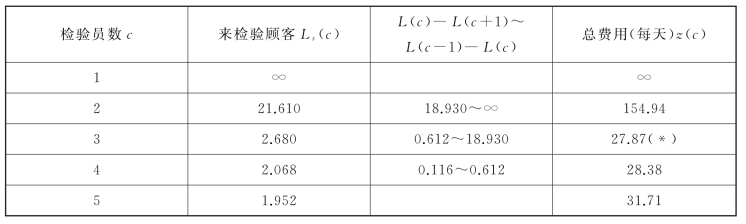
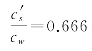,落在区间(0．612~18．930)内,所以c∗＝3。即应设3个检验员使总费用为最小,直接代入式(10-57)也可验证总费用为最小。

z(c∗)＝z(3)＝27．87(元)