如何设置最优服务率μ-M/M/1模型优化

(1)标准的M/M/1模型。

取目标函数z为单位时间服务成本与顾客在系统逗留费用之和的期望值,即

其中,cs为当μ＝1时服务机构单位时间的费用;cw为每个顾客在系统停留单位时间的费用。

根号前取＋号,是因为保证ρ＜1,μ＞λ的缘故。

(2)系统中顾客最大限制数为N的情形。

在这情形下,系统中如已有N个顾客,则后来的顾客即被拒绝,于是:

PN——被拒绝的概率(借用电话系统的术语,称为呼损率);

1－PN——能接受服务的概率;

λ(1－PN)——单位时间实际进入服务机构顾客的平均数。在稳定状态下,它也等于单位时间内实际服务完成的平均顾客数。

设每服务1人能收入G元,于是单位时间收入的期望值是λ(1－PN)G元。

纯利润为:

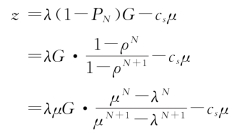
求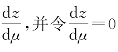,得:(www.xing528.com)

最优的解μ∗应合于上式。上式中cs,G,λ,N都是给定的,但要由上式中解出μ∗是很困难的。通常是通过数值计算来求μ∗的,或将上式左方(对一定的N)作为ρ的函数作出图形(如图10-16所示),对于给定的G/cs根据图形可求出μ∗/λ。

(3)顾客源为有限的情形。

仍按机械故障问题来考虑,设共有机器m台,各台连续运转时间服从负指数分布。有1个修理工人,修理时间服从负指数分布。当服务率μ＝1时的修理费用cs,单位时间每台机器运转可得收入G元。平均运转台数为m－Ls,所以单位时间纯利润为

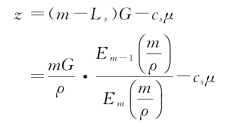
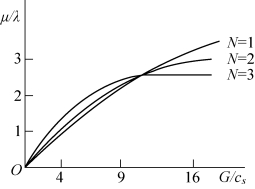
图10-16

式中的

为了求最优服务率μ∗,求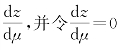,得:

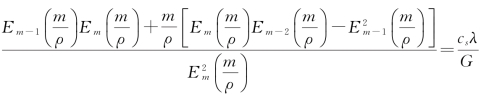
当给定m,G,cs,λ,要由上式解出μ∗是很困难的,通常是利用泊松分布表通过数值计算来求得,或将上式左方(对一定的m)作为ρ的函数作出图形(如图10-17所示),对于给定的csλ/G根据图形可求出μ∗/λ。

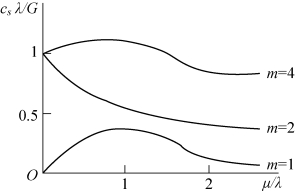
图10-17