【摘要】:设顾客总体(顾客源)为有限数m,且m>c,和单服务台情形一样,顾客到达率λ是按每个顾客来考虑的,在机器管理问题中,就是共有m台机器,有c个修理工人,顾客到达就是机器出了故障,而每个顾客的到达率λ是指每台机器每单位运转时间出故障的期望次数。该系统的状态转移图如图10-13所示。解:m=5,λ=1,μ=4,c=2,cρ/m=λ/μ=1/4。
设顾客总体(顾客源)为有限数m,且m>c,和单服务台情形一样,顾客到达率λ是按每个顾客来考虑的,在机器管理问题中,就是共有m台机器,有c个修理工人,顾客到达就是机器出了故障,而每个顾客的到达率λ是指每台机器每单位运转时间出故障的期望次数。系统中顾客数n就是出故障的机器台数,当n≤c时,所有的故障机器都在被修理,有(c-n)个修理工人在空闲;当c<n≤m时,有(n-c)台机器在停机等待修理,而修理工人都在繁忙状态。假定这c个工人修理技术相同,修理(服务)时间都服从参数为μ的负指数分布,并假定故障的修复时间和正在生产的机器是否发生故障是相互独立的。
该系统的状态转移图如图10-13所示。

图10-13
因ρ=mλ/(cμ),可得:
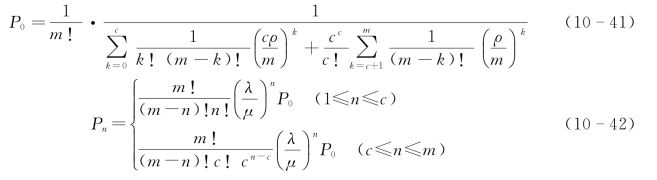
各项指标如下:
①平均队长:

②平均队列长:

平均队长和平均队列长的关系为:

③有效到达率:
![]() (https://www.xing528.com)
(https://www.xing528.com)
④平均逗留时间:

⑤平均等待时间:

【例10-7】设有两个修理工人,负责5台机器的正常运行,每台机器平均损坏率为每运转1小时1次,两工人能以相同的平均修复率4次/小时修好机器。求:
①等待修理的机器平均数;
②需要修理的机器平均数;
③有效损坏率;
④平均等待修理时间;
⑤平均停工时间。
解:
m=5,λ=1(次/小时),μ=4(台/小时),c=2,cρ/m=λ/μ=1/4。

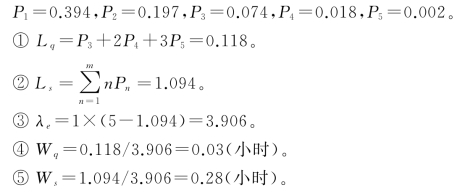
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




