系统容量有限制的情况：M/M/1/N/∞模型

如果系统的最大容量为N,对于单服务台的情形,排队等待的顾客最多为N－1,在某一时刻顾客到达时,如系统中已有N个顾客,那么这个顾客就被拒绝进入系统,如图10-5所示。

图10-5

当N＝1时为即时制的情形;当N→∞,为容量无限制的情形。

若只考虑稳态的情形,可作各状态间概率强度的转换关系图,如图10-6所示。

图10-6

这时系统的状态概率如下:

系统的各种指标:

①队长(期望值):

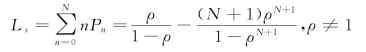
②队列长(期望值):

当研究顾客在系统平均逗留时间Ws和在队列中平均等待时间Wq时,虽然Little公式仍可利用,但要注意平均到达率λ是在系统中有空时的平均到达率,当系统已满(n＝N)时,则到达率为0,因此需要求出有效到达率λe＝λ(1－PN)。可以验证:

③顾客逗留时间(期望值):

④顾客等待时间(期望值):

(www.xing528.com)

现在把M/M/1/N/∞型的指标归纳如下(当ρ≠1时):

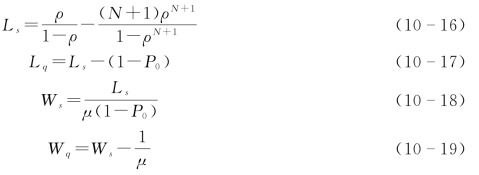
【例10-3】单人理发馆有6个椅子接待人们排队等待理发。当6个椅子都坐满时,后来到的顾客不进店就离开。顾客平均到达率为3人/小时,理发需时平均15分钟,则N＝7为系统中最大的顾客数,λ＝3人/小时,μ＝4人/小时。试求:

①某顾客一到达就能理发的概率;

②需要等待的顾客数的期望值;

③有效到达率;

④一顾客在理发馆内逗留的期望时间;

⑤在可能到来的顾客中不等待就离开的概率(Pn≥7)。

解:

①某顾客一到达就能理发的概率,这种情形相当于理发馆内没有顾客,所求概率为:

②需要等待的顾客数的期望值:

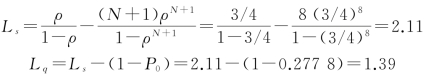
③有效到达率:

④一顾客在理发馆内逗留的期望时间:

⑤在可能到来的顾客中不等待就离开的概率(Pn≥7),即求系统中有7个顾客的概率,这也是理发馆的损失率。