标准的M/M/1模型是指适合下列条件的排队系统:
①输入过程——顾客源是无限的,顾客单个到来,相互独立,一定时间的到达数服从泊松分布,到达过程也是平稳的。
②排队规则——单队,且对队长没有限制,先到先服务。
③服务机构——单服务台,各顾客的服务时间是相互独立的,服从相同的负指数分布。
此外,还假定到达间隔时间和服务时间是相互独立的。
各状态间的转移关系,用图10-4表示。

图10-4
系统状态为n的概率:

公式(10-7)的ρ有其实际意义。根据表达式的不同,可以有不同的解释。当表示为ρ=λ/μ时,它是平均到达率与平均服务率之比,即在相同时区内顾客到达的平均数与被服务的平均数之比。若表示为ρ=(1/μ)/(1/λ),它是为一个顾客的服务时间与到达间隔时间之比,称ρ为服务强度(traffic intensity),或称ρ为话务强度。由式(10-7),ρ=1-P0,它刻画了服务机构的繁忙程度,所以又称服务机构的利用率。
系统的运行指标如下:
①在系统中的平均顾客数(队长期望值):
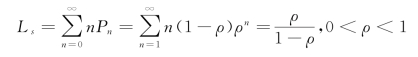
或者
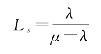
②在队列中等待的平均顾客数(队列长期望值):
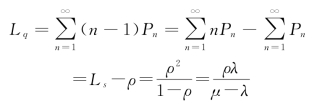
③在系统中顾客平均逗留时间(期望值):

④在队列中顾客平均等待时间(期望值):
![]()
现将以上各式归纳如下:

它们相互的关系如下:

上式称为Little公式。(https://www.xing528.com)
【例10-2】某医院手术室根据病人来诊和完成手术时间的记录,任意抽查了100个工作小时,每小时来就诊的病人数n的出现次数如表10-4所示;又任意抽查了100个完成手术的病历,所用时间v(单位:小时)出现的次数如表10-5所示。试求:
表10-4
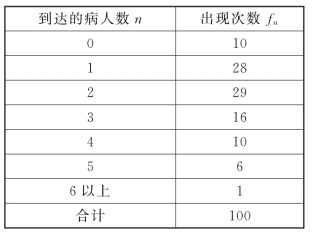
表10-5
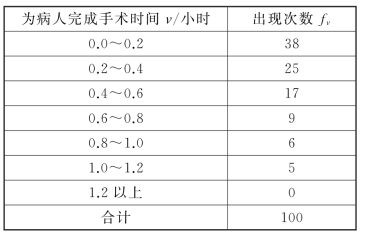
①每小时病人平均到达率;
②每次手术平均时间;
③每小时完成手术人数;
④服务强度ρ;
⑤在病房中的平均病人数;
⑥排队等待的平均病人数;
⑦病人在病房中的平均逗留时间;
⑧病人排队的平均等待时间。
解:
①每小时病人平均到达率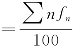 =2.1(人/小时)。
=2.1(人/小时)。
②每次手术平均时间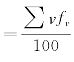 =0.4(小时/人)。
=0.4(小时/人)。
③每小时完成手术人数(平均服务率)=![]() =2.5(人/小时)。
=2.5(人/小时)。
④服务强度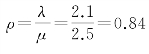 ,说明手术室有84%的时间是繁忙的,有16%的时间是空闲的。
,说明手术室有84%的时间是繁忙的,有16%的时间是空闲的。
⑤在病房中的平均病人数(期望值):
![]()
⑥排队等待的平均病人数(期望值):
![]()
⑦病人在病房中的平均逗留时间(期望值):
![]()
⑧病人排队的平均等待时间(期望值):
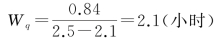
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




