食品削价处理与甲产品生产费用优化问题

9-1 某商店拟在新年期间出售一批日历画片,每张进价1．3元,售价2元。如果在新年期间不能售出,必须削价处理,每张降至0．9元。由于削价,一定可以售完。根据以往的经验,市场需求的概率如表9-5所示。如果每年只能订货一次,问应订购日历画片多少张,才能使获利的期望值最大?

表9-5

9-2 某报亭出售某种报纸,其需求量在5百至1千份之间,需求的概率分布如表9-6所示。又知该报纸每售出一百份利润22元,每积压一百份损失20元,问报亭每天应订购多少份这种报纸,利润最大?

表9-6

9-3 某商店经销某种食品,每周进货一次,无须订货费。该食品为每箱30袋包装,每箱进价21元,每袋售1元。食品保存期为一周,到周末未售出的只能按每袋0．5元削价处理,这时一定可售完。据历年经验,每周市场对该食品的需求如表9-7所示。问商店对该食品每周进货多少最佳?

表9-7

9-4 某商品的需求量x分布如表9-8所示。已知该商品的购进单价为12．5元,出售单价为15元,若当天未能售出,第二天的处理价格为11．25元。试求合理的进货数量。

表9-8

9-5 设某货物的需求量在17~26件,已知需求量x的概率分布如表9-9所示,并知其成本为每件5元,售价为每件10元,处理价为每件2元。问:

表9-9

(1)应进货多少,才能使总利润的期望值最大?

(2)若因缺货造成的损失为每件25元,最佳经济批量又该是多少?

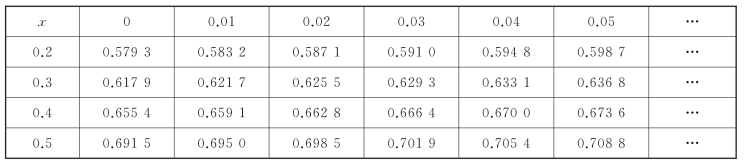
9-6 某食品店内,每天对面包的需求服从μ＝300和σ＝50的正态分布,部分标准正态分布如表9-10所示。已知每个面包的售价为0．5元,成本为每个0．3元,对当天未售出的处理价为每个0．2元。问该食品店每天应生产多少个面包,预期利润最大?

表9-10

续表

9-7 某货物每周的提取量为2 000件,每次订货的固定费用为15元,每件产品每周的保管费为0．3元,求最佳订货批量和订货时间。

9-8 某工厂每年对某种零件的需要量为10 000件,订货的固定费用为2 000元,采购一个零件的单价为100元,保管费为每年每个零件20元,求最优订购批量和最低成本。(www.xing528.com)

9-9 某仓库A商品年需求量为16 000箱,单位商品年保管费为20元,每次订货成本为400元,求经济订货批量Q∗、经济订货周期T∗。

9-10 某轧钢厂每月按计划需产角钢3 000吨,每吨每月需存储费60元,每次生产需调整机器设备等,共需准备费2 500元。按EOQ模型计算最佳生产批量。

9-11 某企业每年要购买100 000只某种零件,有关费用如下:单位价格为0．6元/件,每次订货费用为860元,每个零件的仓库保管费为每月0．15元,试求经济订货批量、年订购次数、年订购总成本、年保管总成本、年库存总成本。

9-12 某批发公司向附近200多家食品零售店提供货源,批发公司负责人为减少存储费用,选择了某种品牌的方便面进行调查研究,以制定正确的存储策略。调查结果如下:

①方便面每周需求3 000箱;

②每箱方便面一年的存储费为6元,其中包括贷款利息3．6元,仓库费、保险费、损耗费、管理费等计2．4元。

③每次订货费25元,其中包括批发公司支付给采购人员的劳务费12元,支付的手续费、电话费、交通费等13元。

④方便面每箱价格30元。一年按50周算。

9-13 某印刷厂每周需要用纸32卷,每次订货费(包括运费等)为250元;存储费为每周每卷10元。问每次订货多少卷,可使总费用最小?

9-14 某商店有甲商品出售,每单位甲商品成本为500元,其存储费每年为成本的20%,该商品每次的订购费为20元,顾客对甲商品的年需求量为360个,如不允许缺货,订货提前期为零,求最佳订购批量、最小费用及最佳订货周期。如果订货方式不按上述办法,而是每隔20天订货一次,每次订购20个,试计算总费用,并对两种结果进行比较。一年按360天计算。

9-15 某厂每月需甲产品100件,每月生产率为500件,每批装配费用为5元,每月每件产品存储费用为4元,求EOQ及最低费用。

9-16 某企业每月需某产品100件,由内部生产解决,设每月生产500件,每批装备费为5万元,每件每月存储费为0．4万元/件。试求最佳生产批量及最佳生产周期,使每月的总费用最少。

9-17 某电视机厂自行生产扬声器用以装配本厂生产的电视机。该厂每天生产100部电视机,而扬声器生产车间每天可以生产500个。已知该厂每批电视机装备的生产准备费为500元,而每个扬声器在一天内的保管费为0．02元。试确定该厂扬声器的最佳生产批量、生产时间和电视机的安装周期。

9-18 某百货公司对格力空调的年需求量为100台,设每次订购费为4元,每台每年存储费为1．5元。如果允许缺货,每台每年缺货损失费为50元,试求最佳订购方案。

9-19 某电子设备厂对一种元件的需求为每年2 000件,不需要提前订货,每次订货费为25元。该元件每件成本为50元,年存储费为成本的20%。如发生供应短缺,可在下批货到时补上,但缺货损失为每件每年30元。

①求经济订货批量及全年的总费用。

②如不允许发生供应短缺,重新求经济订货批量,并与①中的结果比较。

9-20 某厂每年需某种元件300个,每次订购费200元,保管费每件每年100元,不允许缺货。元件单价随采购数量不同而有变化,数量小于50个时,单价500元;数量大于等于50个小于100个时,单价480元;数量大于等于100个时,单价475元。求最佳订购批量。

9-21 某厂每年需某种元件500个,每次订购费50元,保管费每件每年20元,不允许缺货。元件单价随采购数量不同而有变化,数量小于100个时,单价40元;数量大于等于100个小于200个时,单价39元;数量大于等于200个小于300个时,单价38元;数量大于等于300个时,单价37元。求最佳订购批量。

9-22 某公司打算在一年内购买某种物品,订购费50元/次,存储费3元/件,需求量18 000件/年,该物品价格有折扣,当数量小于1 500件时,每件3元;数量大于等于3 000件时,每件2．8元;其他数量时,价格2．9元。试求最佳订货批量、最佳订货周期和最小费用。

9-23 考虑一个具有三种物品的存储问题,有关数据如表9-11所示,已知仓库最大容积为W＝2 400,试求各种物品的最佳订货批量。

表9-11