存储模型中的约束条件优化方案

考虑到仓库容积或资金方面的限制,在存储模型中往往需要增加必要的约束(限制)条件。具有约束条件的存储模型同样假设瞬时进货,不允许缺货。

现假设Qi为第i种(i＝1,2,…,n)物品的订货批量,已知每件第i种物品占用的存储空间为wi,仓库的最大存储量为W,因此在考虑各种物品的订货批量时需要附加约束条件为:

设第i种物品的单位需求率为Di,订购费和存储费分别为C2i和C1i,求使总费用最小的订购批量。

根据以上条件建立具有约束条件的存储模型:

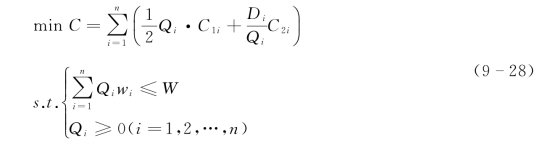
模型求解结果为:

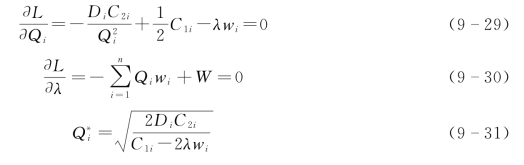
联立公式(9-29)和公式(9-30)可以求出λ。

以上是规范的求解程序,对于实际问题来说,一般先令λ＝0,再根据公式(9-31)求出代入公式(9-27),若满足公式(9-27),计算结束;若不满足,可采用试算法,逐步减少λ值,直到求出的Q∗满足公式(9-27)时为止。

【例9-12】某仓库要存储三种物品,数据如表9-4所示。已知仓库的存储量为W＝30立方米,试求每种物品的经济订货批量?

表9-4

解:

令λ＝0,由题意,根据公式(9-31)计算出三种物品的经济订货批量:

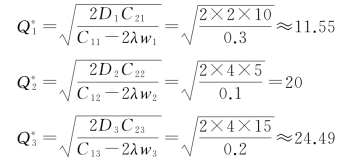
将结果代入公式(9-27):(www.xing528.com)

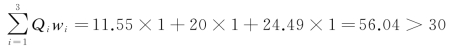
因不满足仓储限制条件,需要逐步减少λ值(本例中每次减少0．05)。

当λ＝－0．05时,计算过程如下:

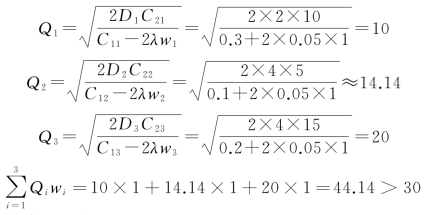
当λ＝－0．1时,计算过程如下:

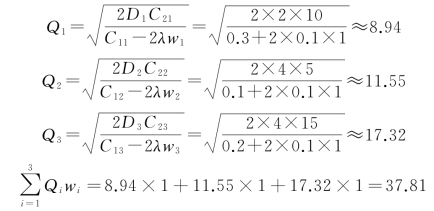
当λ＝－0．15时,计算过程如下:

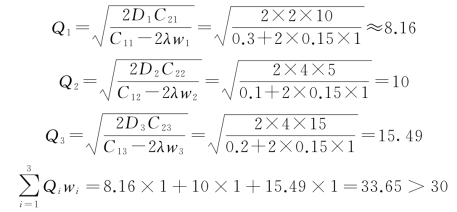
当λ＝－0．2时,计算过程如下:

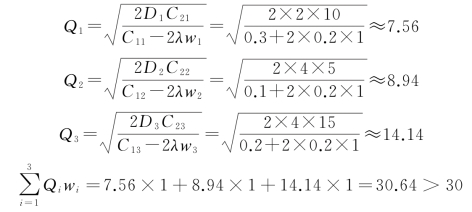
当λ＝－0．25时,计算过程如下:

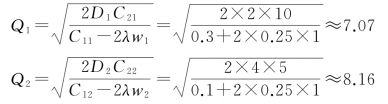
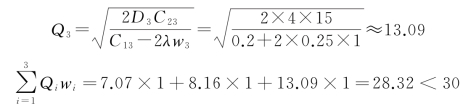
综上,取整后结果为将该结果代入到公式(9-28)中,得:

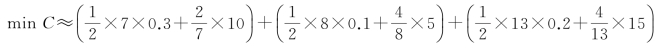
所以,C∗≈3．91＋2．9＋5．92＝12．73。

关于多周期随机型库存模型本教材未做介绍,读者可参考其他教材自学相关内容。