离散型随机变量需求量的存储模型优化

视频-9．2．2 需求量是离散型随机变量的存储模型之报童问题-1

视频-9．2．2 需求量是离散型随机变量的存储模型之报童问题-1举例

视频-9．2．2 需求量是离散型随机变量的存储模型之报童问题-2练习

对于需求量是离散型随机变量的报童问题,X为离散型随机变量,取值为xi,i＝1,2,…,n,概率分布为p(xi)。最优存储策略是该周期内的总期望费用最小或期望收益最大。

当订货批量Q≥xi时,供过于求,费用期望值为:

当订货批量Q＜xi时,供不应求,费用期望值为:

因此,总费用期望值为:

对于离散型随机变量,不能用求导方法求极值,但是E[C(Q)]存在极小值的必要条件为:

据此,可以推导出:

即

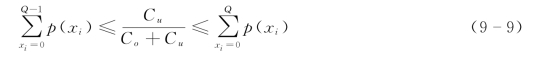
一般利用公式(9-9)来计算Q∗,其中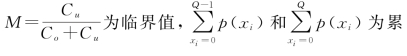加概率。

公式(9-7)和(9-8)的推导过程可以扫码阅读。

【例9-1】某报童每天向邮局订购报纸若干份,若报童一提出订购,立即可拿到报纸。设订购报纸每份0．35元,零售报纸每份0．50元,如果当天没有售完,第二天可退回邮局,邮局按每份0．10元退款。已知这种报纸需求的概率分布如表9-1所示,问报童应订多少份报纸,才能保证损失最少?

离散型随机变量公式推导

表9-1

解:

根据题意,C＝0．35,P＝0．5,V＝0．10,代入公式(9-1)和(9-2)中,有:

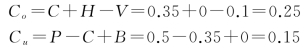
再将Co＝0．25,Cu＝0．15代入公式(9-9)中,有:

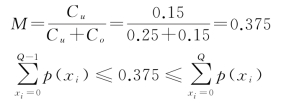(www.xing528.com)

根据表9-1计算累积概率(注意:需求量为其他数值的概率为零):

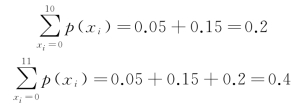
即Q∗－1＝10,Q∗＝11,所以当报童订购11份报纸时,才能保证损失最少。

同时根据公式(9-5),可以计算出当报童订购11份报纸时总费用的期望值为:

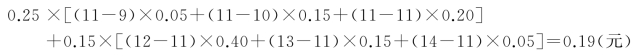
在这种情况下,最大利润期望值为:

【例9-2】某工厂从国外进口150台设备,其中关键备件必须在进口设备时同时购买。该备件订购价为500元,无备件时导致的停产损失和修复费合计10 000元。已知150台设备因关键部件损坏而需要xi个备件的概率分布为p(xi),如表9-2所示。问工厂在购买设备的同时应购买多少关键备件?

表9-2

解:

根据题意,C＝500元,P＝500元,B＝10 000元。

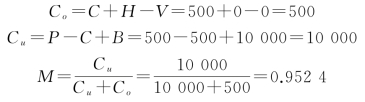
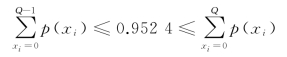
根据表9-2计算累积概率:

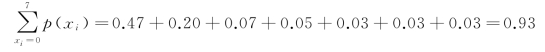
或者

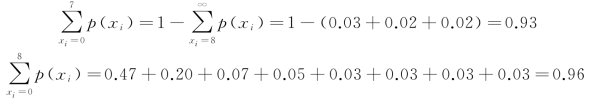
或者

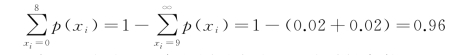
因此,Q∗＝8,即当工厂在购买设备的同时应购买8个关键备件。

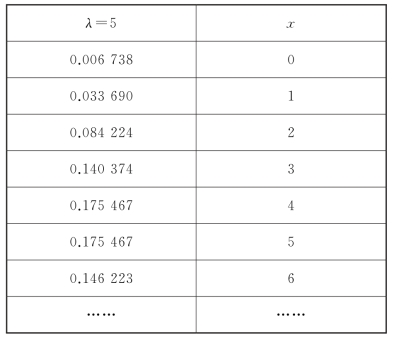
【例9-3】某设备上有一关键零件需要更换,需求量X服从泊松分布,如表9-3所示,根据以往的经验,平均需求量为5件,此零件的价格为100元/件。若零件用不完,到期末完全报废;若备件不足,待零件损坏后再去购买,就会造成停工损失180元。问确定期初应准备多少个配件最好?

表93

解:

根据题意,C＝100,B＝180,V＝0,P＝100(设备成本)。

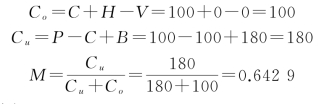
由于服从泊松分布,则有:

根据表9-3计算累积概率,可知Q∗＝6,所以期初最好准备6个配件。