逆序解法：最短路径动态规划的高效解法

(1)建模。

阶段k:第k个阶段选路的过程,k＝5,4,3,2,1。

状态Sk:第k阶段初所处的位置。

决策变量xk:第k阶段选择的路径。

阶段指标Vk:第k阶段所选择的路径对应的路权。

指标函数:Vk(Sk,xk)。

最优函数:fk(Sk)。

动态规划基本方程:

视频-8．2．1 最短路动态规划求解-1-逆序解法

(2)求解。

第一步,如图8-1所示,该最短路问题可划分为五个阶段,边界条件为f6(F)＝0,说明从F点(终点)到F点的最短距离为0,如图8-2所示。

图8-2

第二步,在第四阶段,当k＝5时,状态可能集为S5＝{E1,E2}。

决策允许集为X5(E1)＝{E1 F},X5(E2)＝{E2 F}。

最优函数为f5(E1)＝E1 F＋f6(F)＝12＋0＝12,f5(E2)＝E2 F＋f6(F)＝13＋0＝13,即第五阶段的最优策略为E1→F,如图8-3所示。

图8-3

第三步,当k＝4时,状态可能集为S4＝{D1,D2,D3}。决策允许集为X4(D1)＝{D1 E1},(www.xing528.com)

X4(D2)＝{D2 E1,D2 E2},X4(D3)＝{D3 E2}。

对于状态D1,最优函数为f4(D1)＝min{D1 E1＋f5(E1)}＝min{10＋12}＝22,即第四阶段D1状态下的最优策略为D1→E1→F。

对于状态D2,最优函数为f4(D2)＝min{D2 E1＋f5(E1),D2 E2＋f5(E2)}＝min{9＋12,7＋13}＝20,即第四阶段D2状态下的最优策略为D2→E2→F。

对于状态D3,最优函数为f4(D3)＝min{D3 E2＋f5(E2)}＝min{9＋13}＝22,即第四阶段D3状态下的最优策略为D3→E2→F,如图8-4所示。

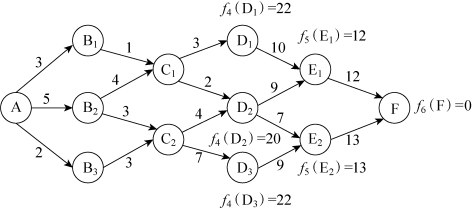
图8-4

第四步,当k＝3时,状态可能集为S3＝{C1,C2}。决策允许集为X3(C1)＝{C1 D1,C1 D2},X3(C2)＝{C2 D2,C2 D3}。

对于状态C1,最优函数为f3(C1)＝min{C1 D1＋f4(D1),C1 D2＋f4(D2)}＝min{3＋22,2＋20}＝22,即第三阶段C1状态下的最优策略为C1→D2→E2→F。

对于状态C2,最优函数为f3(C2)＝min{C2 D2＋f4(D2),C2 D3＋f4(D3)}＝min{4＋20,7＋22}＝24,即第三阶段C2状态下的最优策略为C2→D2→E2→F,如图8-5所示。

图8-5

第五步,当k＝2时,状态可能集为S2＝{B1,B2,B3}。决策允许集为X2(B1)＝{B1 C1},X2(B2)＝{B2 C1,B2 C2},X2(B3)＝{B3 C2}。

对于状态B1,最优函数为f2(B1)＝min{B1 C1＋f3(C1)}＝min{1＋22}＝23,即第二阶段B1状态下的最优策略为B1→C1→D2→E2→F。

对于状态B2,最优函数为f2(B2)＝min{B2 C1＋f3(C1),B2 C2＋f3(C2)}＝min{4＋22,3＋24}＝26,即第二阶段B2状态下的最优策略为B2→C1→D2→E2→F。

对于状态B3,最优函数为f2(B3)＝min{B3 C2＋f3(C2)}＝min{3＋24}＝27,即第二阶段B3状态下的最优策略为B3→C2→D2→E2→F,如图8-6所示。

图8-6

第六步,当k＝1时,状态可能集为S1＝{A}。决策允许集为X1(A)＝{AB1,AB2,AB3}。如图8-7所示。

图8-7

综上,最优函数为f1(A)＝min{AB1＋f2(B1),AB2＋f2(B2),AB3＋f2(B3)}＝min{3＋23,5＋26,2＋27}＝26,第一阶段A状态下的最优策略为A→B1→C1→D2→E2→F,即最短路径,最短路权为26。