解决非确定性统筹问题的方法与实践

以上所考虑的工序时间是属于确定性的,在实际中往往不是这样的。例如,在研制一种新的发展项目时,许多工序时间几乎没有什么可供参考的资料,或因干扰因素过多无法确定工序时间,这样就产生了非确定性统筹问题。解决非确定性统筹问题,需要把不确定的工序时间化为确定的工序时间,再编制工程进度计划和绘制统筹图,这就是计划评审技术(PERT)。对于非确定性统筹问题的工序时间,一般采用三时估计法,对于非确定性统筹问题而言,重要的是这种估计的可靠性如何。

(1)三时估计法。

在影响工序因素较多,工序持续时间难以准确估计时,可以采用三时估计法来确定工序时间。假设a为最快可能完成的时间;m为最可能完成的时间;b为最慢可能完成的时间。在一般情况下,可按下列公式近似估算工序时间:

(2)估计的可靠性。

在工序时间不确定的条件下,如果已对各工序作了三时估计,得到工序时间的估计值E[t(i,j)],并根据公式算出方差,那么将该估计值E[t(i,j)]当作实际工序时间看待,就可绘制出网络图,找出关键线路。由于工程的总工期是由所有关键工序的工序时间之和求得的,但这里的工序时间都是随机变量,因此总工期也是随机变量,也存在总工期的期望值E(Te)与方差D(Te)。

由于工序是相互独立的,因此总工期Te的期望值应该等于关键线路中所有关键工序的工序时间期望值之和,总工期Te的方差应该等于关键线路中所有关键工序的工序时间的方差之和,即

【例7-6】某工程各工序及持续时间的三时估计如表7-5所示,试求工程的E(Te),D(Te)和标准差σ2(Te)。

表7-5

解:

根据公式(7-9)和公式(7-10),计算出工序时间的估计值E[t(i,j)]和σ2[t(i,j)],如表7-6所示。(www.xing528.com)

表7-6

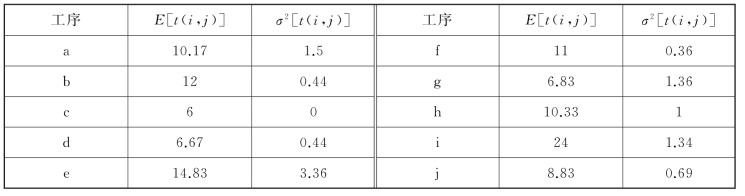
再根据表7-5所给出的各工序之间的逻辑关系,画出网络图,如图7-39所示。

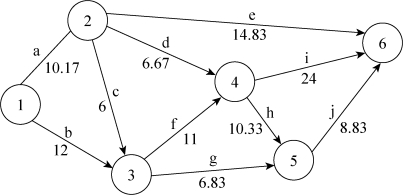
图7-39

计算工序的时间参数并确定关键线路:

由关键工序a,c,f和i的工序时间的期望值,求出总工期的期望值为:

E(Te)＝E[t(1,2)]＋E[t(2,3)]＋E[t(3,4)]＋E[t(4,6)]＝10．17＋6＋11＋24＝51．17(天)

总工期的方差为:

D(Te)＝σ2[t(1,2)]＋σ2[t(2,3)]＋σ2[t(3,4)]＋σ2[t(4,6)]＝1．5＋0＋0．36＋1．34＝3．2

总工期的标准差为:

在【例7-6】中,如果Te服从正态分布,期望值为51．17,标准差为1．79,查正态分布表可知,总工期变化在距期望值一个标准差以内的概率为0．68,在距期望值3个标准差之内的概率为0．997,即工期在(51．17±1．79)天区间内完成的可能性为68%,工期在(51．17±3×1．79)天区间内完成的可能性为99．7%。