如何优化工期与费用？

视频-7．3．2 网络计划优化1

视频-7．3．2 网络计划优化2

视频-7．3．2 网络计划优化3

视频-7．3．2 网络计划优化4

工期-费用优化,即工期成本优化或者时间成本优化,是指寻求工程总成本最低时的工期或按要求工期寻求最低成本的计划安排。

(1)费用和工期的关系。

总费用＝直接费用＋间接费用,如图7-27所示。

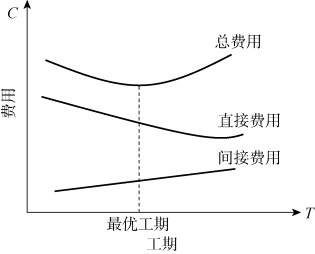
图7-27

(2)方法与步骤。

①按工作正常持续时间画出计划网络图,找出关键线路、工期、总费用;

②计算各工作的直接费用率ΔCi－j;

③压缩工期;

④计算压缩后的总费用为CT′＝CT＋ΔCi－j×ΔTi－j－间接费用率×ΔTi－j;

⑤重复步骤③、④,直到总费用最低。

压缩工期时应注意:压缩关键工序的持续时间,不能把关键工序压缩成非关键工序;当同时压缩几项关键工序时,需要选择直接费用率或直接费用率组合最低的关键工序,且其值应不超过间接费率。

【例7-4】已知某工程计划网络图如图7-28所示。箭线上方括弧外数字表示正常时间直接费用,括弧内数字表示最短时间直接费用;箭线下方括弧外数字表示正常持续时间,括弧内数字表示最短持续时间。已知整个工程计划的间接费用率为0．35万元/天,正常工期时的间接费用为14．1万元。试对此计划进行费用优化,求出费用最少的工期。

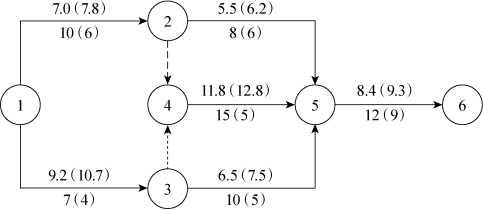
图7-28

解:

①通过计算,得出关键线路为①→②→④→⑤→⑥,如图7-29加粗部分所示。工期T＝37天,总费用＝直接费用＋间接费用＝(7．0＋9．2＋5．5＋11．8＋6．5＋8．4)＋14．1＝62．5(万元)。(www.xing528.com)

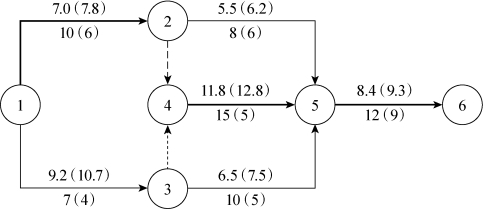
图7-29

②计算各工作的直接费用率ΔCi－j,结果如表7-4所示,将直接费用率标在图7-30中。

表7-4

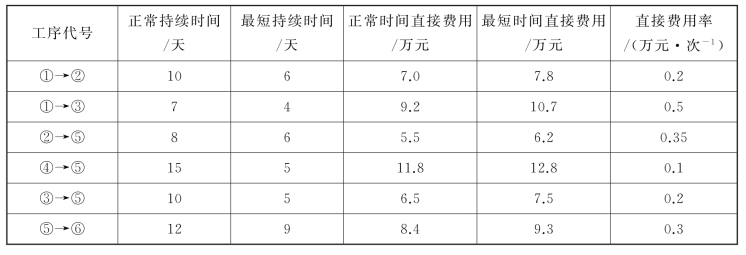
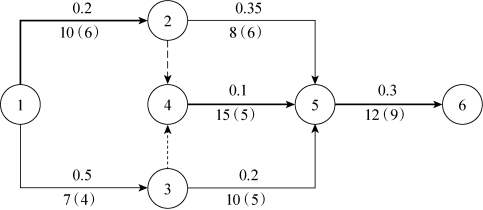
图7-30

③压缩工期。

第一次优化:选择工序④→⑤,压缩7天,成为8天,工期变为30天,②→⑤也变为关键工序,如图7-31所示。

图7-31

第一次优化后的总费用为:

c′T＝CT＋ΔCi－j×ΔTi－j－间接费用率×ΔTi－j＝62．5＋0．1×7－0．35×7＝60．75(万元)

第二次优化:选择工序①→②,压缩1天,成为9天,工期变为29天,工序①→③和③→⑤也变为关键工序,如图7-32所示。

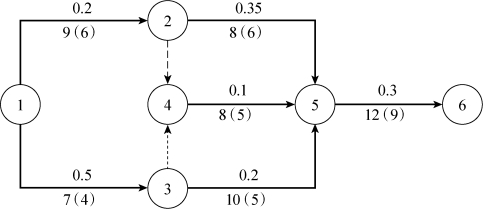
图7-32

第二次优化后的总费用为:

c′T＝CT＋ΔCi－j×ΔTi－j－间接费用率×ΔTi－j＝60．75＋0．2×1－0．35×1＝60．6(万元)

第三次优化:选择工序⑤→⑥,压缩3天,成为9天,工期变为26天,关键工序没有发生变化,如图7-33所示。

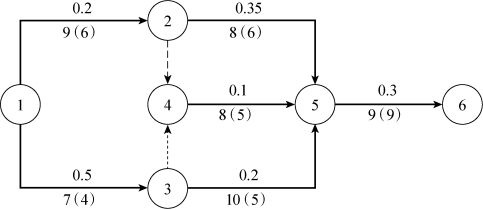
图7-33

第三次优化后的总费用为:

c′T＝CT＋ΔCi－j×ΔTi－j－间接费用率×ΔTi－j＝60．6＋0．3×3－0．35×3＝60．45(万元)

第四次优化:选择直接费用率最小的组合①→②和③→⑤,其值为0．4万元/天,大于间接费用率0．35万元/天,若再压缩,会使费用增加。

因此,最优工期为26天,费用为60．45万元。优化效果是减少了11天和2．05万元。