城市道路连通性与考试日程安排，最小树求解与最短路径问题

6-1 已知16个城市及它们之间的道路联系如图6-56所示,某旅行者从城市A出发,沿途经过J,N,H,K,G,B,M,I,E,P,F,C,L,D,O,C,G,N,H,K,O,D,L,P,E,I,F,B,J,A,最后到达城市M。由于疏忽,该旅行者忘记在图上标明各城市的位置。请用图的基本概念及理论,在图6-56中标明各城市A~P的位置。

图6-56

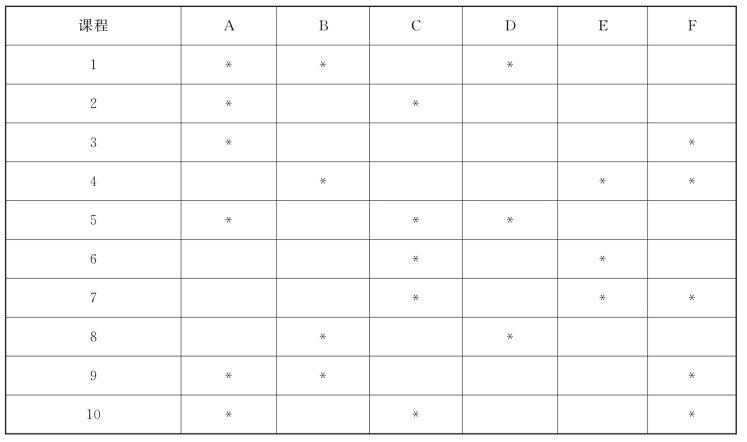
6-2 10名研究生参加6门课程的考试,如表6-4所示,“∗”表示每个研究生参加考试的课程,规定考试在3天内结束,每天上午和下午各安排一门。研究生提出希望每人每天最多考一门,并且课程A必须安排在第一天上午考,课程F必须安排在最后一门考,课程B只能安排在下午考。试列出一张满足各方面要求的考试日程表。

表6-4

6-3 分别用破圈法和避圈法(加边法)求图6-57中的最小树。

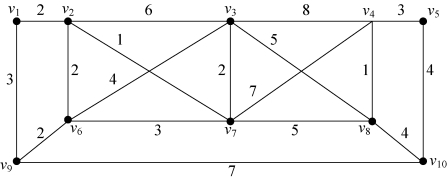
图6-57

6-4 求解图6-58、图6-59、图6-60中的最小树(破圈法)以及从vs到vt的最短路径和最短路权。

(1)

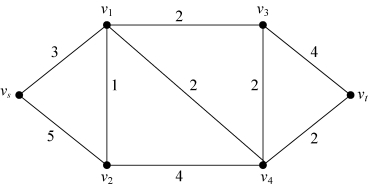
图6-58

(2)

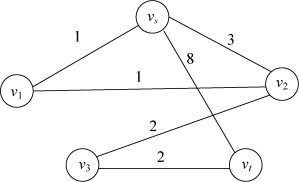
图6-59

(3)

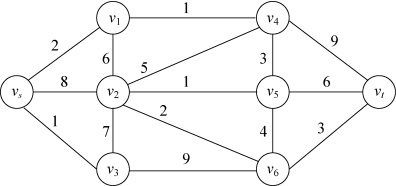
图6-60

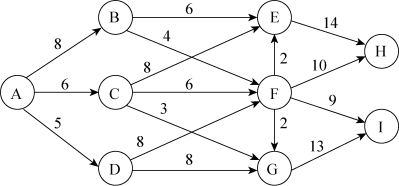
6-5 分别求图6-61中从A到H和I的最短路径和最短路权,并对结果进行比较。

(www.xing528.com)

图6-61

6-6 求图6-62和图6-63中v1到其他点的最短路径和最短路权。

(1)

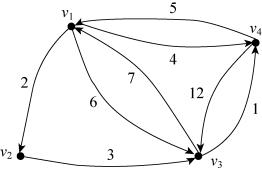
图6-62

(2)

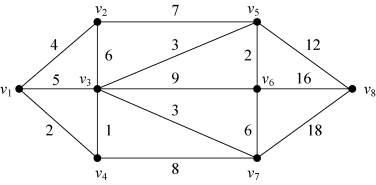
图6-63

6-7 某企业长期使用一台设备加工某一零件,每年年初企业负责人都需要做出如下决策:购置新设备还是继续使用旧设备?已知购置费和维修费如表6-5和表6-6所示(单位均为万元),请制订一个5年内的设备更新计划,使总费用最少。

表6-5

表6-6

6-8 求图6-64和图6-65中从vs到vt的最大流并找出网络“瓶颈”。

(1)

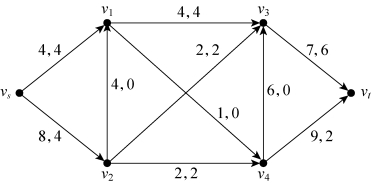
图6-64

(2)

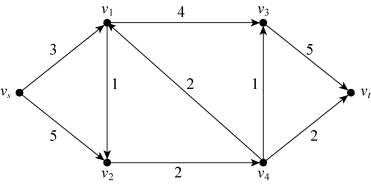
图6-65