割集和最小割集简介

对于网络N＝(V,A,C),将V分为两个非空集合S和S′,且S∩S′＝Ø,使发点vs∈S,收点vt∈S′,则发点属于S而收点属于S′的弧的集合称为割集(S,S′),也称截集。割集(S,S′)中所有前向弧的容量之和r(S,S′)称为割量,割量最小的割集称为最小割集。在网络中,最大流等于最小割集的容量,即最大流—最小割定理。可见,最小割量的大小影响总的流量。

【例6-8】找出图6-35中所有割集。

视频-6．4．3最大流-1割集

解:

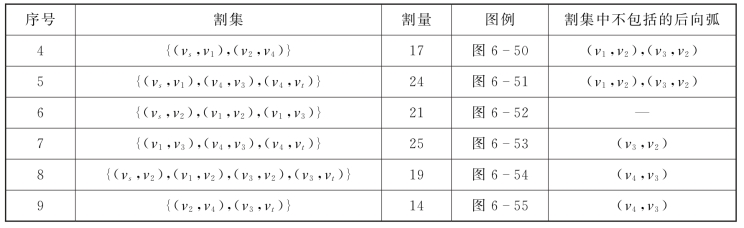
根据割集的定义,只要将图中的发点和收点分开,所截的前向弧就构成割集。按照这个思路可以找到图6-35中所有割集,过程如图6-47~图6-55所示,所得到的割集如表6-3所示。

在寻找割集时,只需考察被截断的弧,选择相关的参照点,判断前向弧和后向弧。参照点为截线的左侧(左上或左下),对于某一参照点,流出的弧为前向弧,流入的弧为后向弧。

视频-6．4．3最大流-2最小割集

在图6-48中,以v1为参照点,(v1,v3)是前向弧(流出)。以v2为参照点,(v2,v4)为前向弧(流出),(v3,v2)为后向弧(流入)。同时,从被割的左半部分,看不到源头v3。

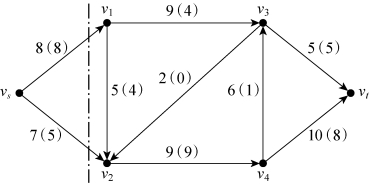
图6-47

图6-48

在图6-50中,以vs为参照点,(vs,v1)是前向弧。以v2为参照点,(v2,v4)为前向弧(流出),(v1,v2)和(v3,v2)为后向弧(流入)。由于被割断,看不到点v1和v3。

在图6-51中,以vs为参照点,(vs,v1)是前向弧。以v2为参照点,(v1,v2)和(v3,v2)为后向弧(流入)。以v4为参照点,(v4,v3)和(v4,vt)为前向弧(流出)。

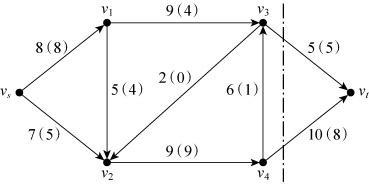
图6-49

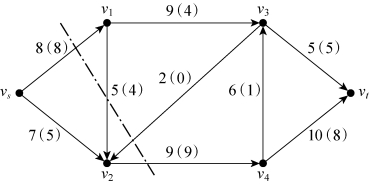
图6-50

(www.xing528.com)

图6-51

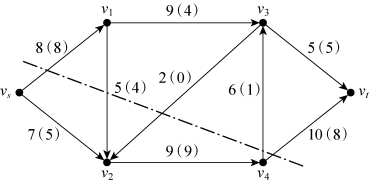
在图6-52中,以vs为参照点,(vs,v2)是前向弧。以v1为参照点,(v1,v2)和(v1,v3)为前向弧(流出)。

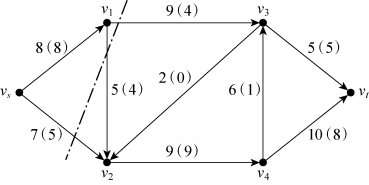
图6-52

在图6-53中,以v1为参照点,(v1,v3)是前向弧(流出)。以v2为参照点,(v3,v2)为后向弧(流入)。以v4为参照点,(v4,v3)和(v4,vt)为前向弧(流出)。

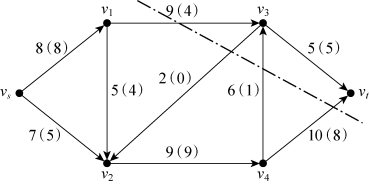
图6-53

在图6-54中,以vs为参照点,(vs,v2)是前向弧(流出)。以v1为参照点,(v1,v2)为前向弧(流出)。以v3为参照点,(v3,v2)和(v3,vt)为前向弧(流出),(v4,v3)为后向弧(流入)。

图6-54

在图6-55中,以v2为参照点,(v2,v4)是前向弧(流出)。以v3为参照点,(v3,vt)为前向弧(流出),(v4,v3)为后向弧(流入)。

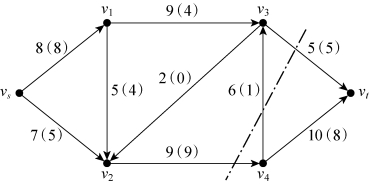
图6-55

从表6-3中也可以看出,最小割集为{(v2,v4),(v3,vt)},最小割量为14。

表6-3

续表

上述寻找割集的方法过于烦琐,可以使用简单的方法,就是用一条曲线(或直线)将得到标号的点和得不到标号的点分开,所截得的前向弧的集合就是最小割集。

对于【例6-8】,首先用双标号法求出最大流,如图6-42所示。用一条曲线将已标号的点和未标号的点分开,则得到最小割集为:{(v2,v4),(v3,vt)},最小割量为14。