求解最大流的标号算法优化

1956年,福特和富尔克逊提出了寻求网络最大流的基本方法,称为福特—富尔克逊算法(Fold-Fulkerson Algorithm),该方法适用于求解弧权非负的最大流问题,求解过程如下:

(1)标号。

视频-6．4．2最大流-4求解

对于一个给定可行流f＝{xij},可以通过标号判断有无增广链,步骤如下:

①对发点vs标号“(＋vs,∞)”,“vs”表示路径是从vs到vs,“＋”表示vs→vs为前向弧,“∞”为流量调整的上限,其余点未做标号。

②考察与发点vs相邻的点vi,(vs,vi)一般为前向弧,若(vs,vi)可以扩充流量,即xsi＜csi,则对vi进行标号“(＋vs,θsi)”,此时流量的调整值为θsi＝csi－xsi。

③考察与vi相邻的点vj(尚未标号)。vj得到标号必须满足以下条件:若(vi,vj)为前向弧且xij＜cij,则对vj进行标号“(＋vi,θij)”,流量的调整值为θij＝min{θsi,cij－xij};若(vi,vj)为后向弧且xij＞0,则对vj进行标号“(－vi,θij)”,流量的调整值为θij＝min{θsi,xij}。

④重复步骤③。若收点vt得到标号,则存在可以扩充流量的路(增广链),说明当前的可行流不是最大流,则进行步骤②;若vt得不到标号,则不存在可以扩充流量的路(增广链),说明当前的可行流是最大流。

(2)流量调整。

考察增广链μ的所有弧,调整其流量。对于前向弧μ＋,流量调整值为θ＝min{cij－xij};对于后向弧μ－,流量调整值为θ＝min{xij}。调整后的流量为:对于前向弧μ＋,xij＋θ;对于后向弧μ－,xij－θ。此时得到新的可行流f′＝{x′ij},再重复步骤①和②,直至获得最大流。

【例6-6】求图6-35中的网络最大流,弧权表示容量(流量)。

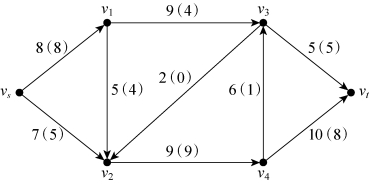
图6-35

解:

第一步,对发点vs标号(＋vs,∞),考察与vs相邻的点v1和v2,前向弧vs→v1饱和,不满足标号条件,因此只对v2进行标号(＋vs,2),其中,“2”是“∞”和“7－5”的最小值,如图6-36所示。

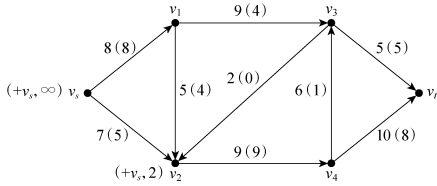
图6-36

第二步,考察与v2相邻的点v1,v3和v4,前向弧v2→v4饱和,后向弧v2→v3为零弧,均不满足标号条件。对于后向弧v2→v1,因流量非零,故可对v1进行标号(－v2,2),其中,“2”是“2”和“4”的最小值,如图6-37所示。

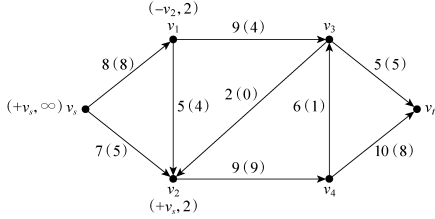
图6-37

第三步,考察与v1相邻且未做标号的点v3,前向弧v1→v3没有饱和,因此可对v3进行标号(＋v1,2),其中,“2”是“2”和“9－4”的最小值,如图6-38所示。

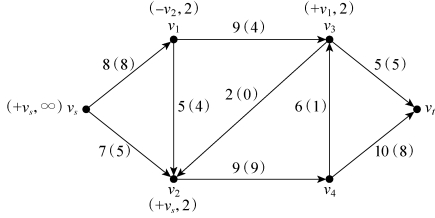
图6-38(www.xing528.com)

第四步,考察与v3相邻且未做标号的点v4和vt,前向弧v3→vt饱和,不满足标号条件。对于后向弧v3→v4,因流量非零,故可对v4进行标号(－v3,1),其中,“1”是“2”和“1”的最小值,如图6-39所示。

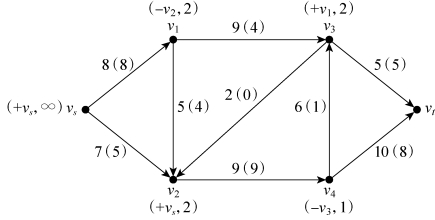
图6-39

第五步,考察与v4相邻且未做标号的点vt,前向弧v4→vt未饱和,满足标号条件。因此可对vt进行标号(＋v4,1),其中,“1”是“1”和“10－8”的最小值,如图6-40所示。

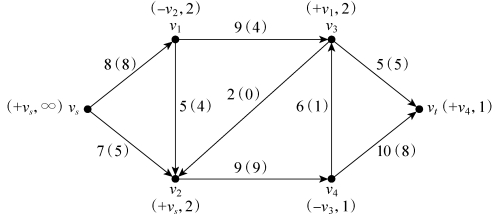
图6-40

第六步,因收点vt得到标号,故该网络存在增广链vs→v2→v1→v3→v4→vt,流量可以扩充,前向弧(vs,v2)、(v1,v3)和(v4,vt)均增加一个流量,后向弧(v2,v1)和(v3,v4)均减少一个流量,调整后的流量增加至14,如图6-41所示。

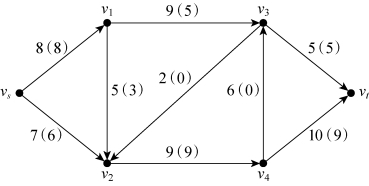
图6-41

第七步,对图6-41进行标号,结果如图6-42所示。由于收点vt得不到标号,故不存在增广链,最大流等于发点的流出量(8＋6＝14)或收点的流入量(5＋9＝14)。

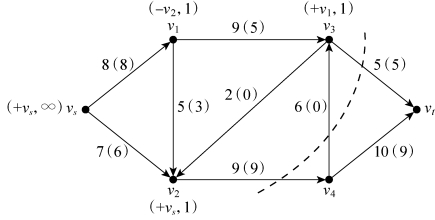
图6-42

【例6-7】求图6-43中的网络最大流。弧权表示容量。

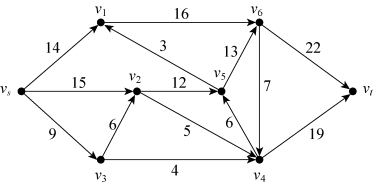
图6-43

解:

假设初始可行流为零,因此可逐渐增加可行流,然后再用双标号法算出最大流。选择路径vs→v1→v6→vt,流量增加“14”;选择路径vs→v3→v4→vt,流量增加“4”;选择路径vs→v3→v2→v4→vt,流量增加“5”;选择路径vs→v2→v5→v6→vt,流量增加“8”。流量增加过程如图6-44所示,得到可行流后进行标号,如图6-45所示,由于收点得到标号,因此方案非最大流方案(31)。

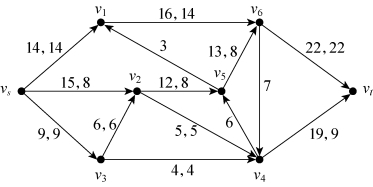
图6-44

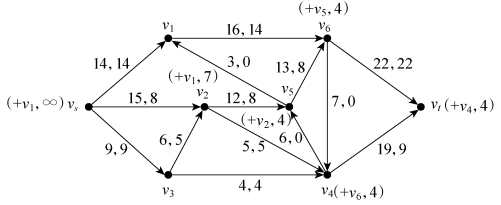
图6-45

调整方案如图6-46所示,再对该方案进行标号,由于收点得不到标号,因此获得最大流方案(35)。

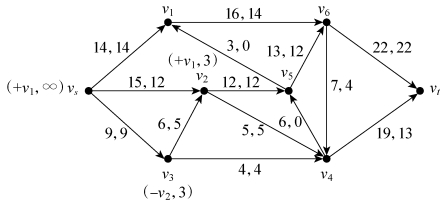
图6-46