求解有向图的最短路算法

视频-6．3．2最短路-1

视频-6．3．2最短路-2

视频-6．3．2最短路-3

对于有向图最短路问题,计算步骤与求解无向图最短路问题相同,主要区别在于:无向图最短路问题使用单标号法,单标号法是对每一点赋予一个路权标号;而有向图最短路问题使用双标号法,双标号法是对每一点赋予两个标号:路径和路权。

【例6-5】用双标号法求解图6-27中从vs到vt的最短路。

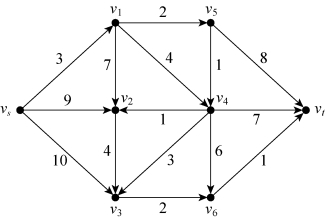
图6-27

解:

第一步,对始点做P标号,其他点做T标号,如图6-28所示。

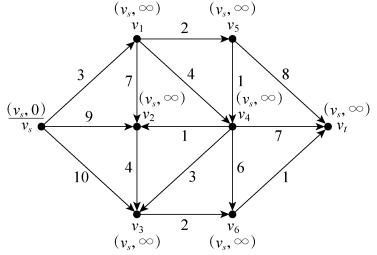
图6-28

第二步,考察点vs的相邻点(即从vs出发可以到达的点v1,v2和v3),修改v1,v2和v3的T标号,然后比较所有已做T标号的点,对路权最小的点v1进行P标号,如图6-29所示。修改T标号的原则:若新的路权小于原路权,则修改标号,若新的路权等于或大于原路权,则不修改。

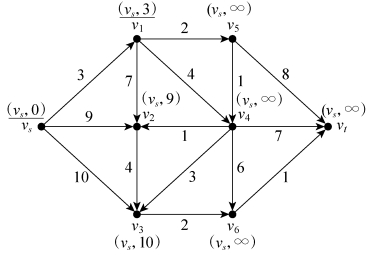
图6-29

第三步,考察点v1的相邻点(v2,v4和v5),修改v4和v5的T标号,由于vs→v1→v2的路权(10)大于原路权(9),所以不修改v2标号,然后比较所有已做T标号的点,对路权最小的点v5进行P标号,如图6-30所示。

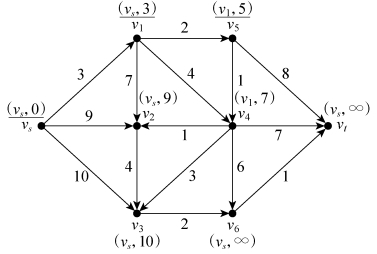(www.xing528.com)

图6-30

第四步,考察点v5的相邻点(v4和vt),修改v4和vt的T标号,然后比较所有已做T标号的点,对路权最小的点v4进行P标号,如图6-31所示。

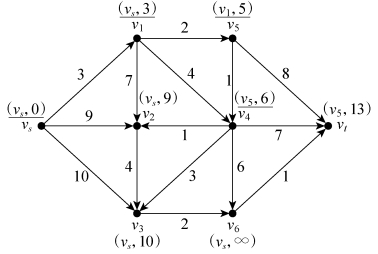
图6-31

第五步,考察点v4的相邻点(v2,v3,v6和vt),修改v2,v3和v6的T标号,因新路权与原路权相等,则不修改vt的T标号,比较所有已做T标号的点,对路权最小的点v2进行P标号,如图6-32所示。

图6-32

第六步,考察点v2的相邻点(v3),不用修改T标号,再对点v3进行P标号。考察点v3的相邻点v6,修改点v6的T标号,再对点v6进行P标号,最后对点vt做P标号,如图6-33所示。

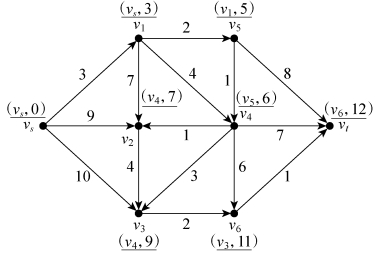
图6-33

反向追踪,可以得到从vs到vt的最短路径为vs→v1→v5→v4→v3→v6→vt,最短路权为12,同时,从始点到其他各点的最短路径和最短路权为:

vs→v1:vs→v1(3);

vs→v2:vs→v1→v5→v4→v2(7);

vs→v3:vs→v1→v5→v4→v3(9);

vs→v4:vs→v1→v5→v4(6);

vs→v5:vs→v1→v5(5);

vs→v6:vs→v1→v5→v4→v3→v6(11)。

注意:对于双标号(左、右),左边元素表示路径,是该结点的前一个结点,右边元素表示路权,表示从始点到该点的总路权。