图论基础：环、多重边、悬挂点及权的概念

(1)关联边。

在无向图中,若vi和vj是边e的两个结点,称e是vi和vj的关联边。例如,在图6-6中,e1是v1和v2的关联边。

(2)相邻。

若vi和vj与同一关联边相连,则称点vi和vj相邻;若边ei和ej有共同的结点,则称边ei和ej相邻。例如,在图6-6中,点v1和v2关于边e1相邻,边e2和e3关于点v3相邻。

(3)环。

若一条边e的两个结点相重叠,称e为环。在图6-6中,边e8首尾相接,因此称为环。

(4)多重边。

若两点之间存在两条以上关联边,则称该两点具有多重边。在图6-6中,边e4和e5是关于点v2和v4的多重边。

(5)多重图。

含多重边的图称为多重图,图6-6为多重图。

(6)简单图。

不含环和多重边的图称为简单图。

(7)次。

点vi关联边的个数,称为点vi的次,也称度,一般记为d(vi)。一个环计算两个次(或度)。(www.xing528.com)

(8)奇点和偶点。

次为奇数的点称为奇点,次为偶数的点称为偶点。

(9)悬挂点和孤立点。

次为1的点称为悬挂点,悬挂点的关联边为悬挂边。次为0的点称为孤立点。

(10)权。

与边或弧相关的数量指标称为权,如距离、费用、流量。

(11)赋权图。

点、边、权的总体称为赋权图。

(12)完全图、子图和支撑子图。

对于一个简单图,若图中任意两点之间均有边相连,则称为完全图。图6-8(a)为完全图(G1＝[V1,E1])。对于G2＝[V2,E2][图6-8(b)],如果V2⊆V1,E2⊆E1,则称G2是G1的一个子图;若V3＝V1,E3⊆E1,则称G3是G1的一个支撑子图[图6-8(c)]。

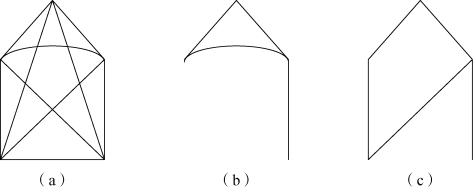
图6-8 完全图、子图和支撑子图

(13)网络。

规定起点、终点和中间点的连通赋权图称为网络,包括有向网络、无向网络和混合网络。