【摘要】：图论中的图与一般几何图形不同,是由一些点和连接点的线所组成的“图形”。例如,图6-2、、均可表示苏州v1、杭州v2、上海v3、南京v4 4个仓储网点之间的物流运输线路。图6-2又例如,图6-3、均可表示赵、钱、孙、李、周、吴、陈7个人之间相互认识的关系。表6-1解:根据题意,运动员甲、乙、丁、戊报名参加第1个比赛项目A,只有丙和己才可以参加第2个项目C的比赛,如表6-1所示。因此,至少需要3个储藏室。
图论中的图与一般几何图形不同,是由一些点(vi)和连接点的线(ej)所组成的“图形”。图中点和线的位置是任意的,线的曲直、长短与实际无关,代表的只是点与点之间的相互关系。例如,图6-2(a)、(b)、(c)均可表示苏州v1、杭州v2、上海v3、南京v4 4个仓储网点之间的物流运输线路。
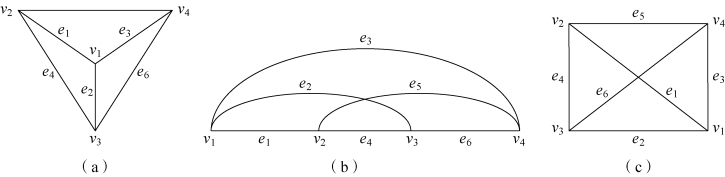
图6-2
又例如,图6-3(a)、(b)均可表示赵、钱、孙、李、周、吴、陈7个人之间相互认识的关系。
图6-3
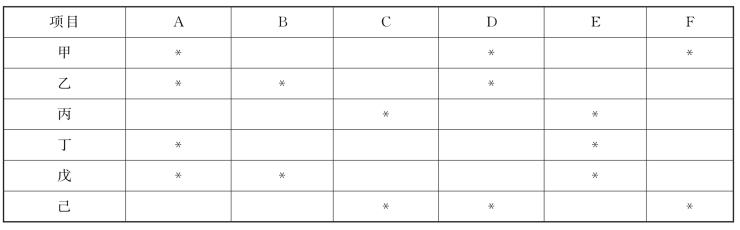
【例6-1】有甲、乙、丙、丁、戊、己6名运动员报名参加A,B,C,D,E,F 6个项目的比赛。报名情况见表6-1中的“∗”,若要求第1个比赛项目为A,且每名运动员不连续参加两个项目的比赛,问:应如何安排比赛顺序?请画图说明。
表6-1
(www.xing528.com)
解:
根据题意,运动员甲、乙、丁、戊报名参加第1个比赛项目A,只有丙和己才可以参加第2个项目C的比赛,如表6-1所示。同理,第3个项目为B,第4个项目为F,第5个项目为E,第6个项目为D。比赛顺序为A→C→B→F→E→D,如图6-4所示。
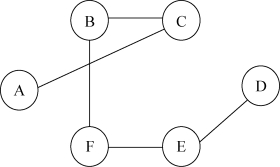
图6-4
【例6-2】某医院需对A,B,C,D,P,R,S,T 8种药品进行保管,为了安全起见,下列14组药品不能存放在同一储藏室内:A-R,A-C,A-T,R-P,P-S,S-T,T-B,B-D,D-C,R-S,R-B,P-D,S-C,S-D,问:存放这8种药品至少需要几个储藏室?
解:
如图6-5所示,因S,P,R三点两两相邻,故三种药品应单独存放。其中,与S不相邻、且彼此也不相邻的点有A,B;与P不相邻、且彼此也不相邻的点有D,T;点C与P不相邻,可与P放在一起。因此,至少需要3个储藏室。
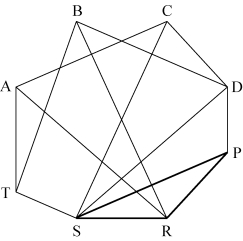
图6-5
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
