目标规划问题的图解求解及单纯形法分析

5-1 某公司生产甲、乙两种产品,分别由Ⅰ,Ⅱ两个车间生产。已知除外购外,生产一件甲产品需要Ⅰ车间加工4小时,Ⅱ车间装配2小时;生产一件乙产品需要Ⅰ车间加工1小时,Ⅱ车间装配3小时,这两种产品生产出来以后均需要经过检验和销售等环节。已知每件甲产品的检验和销售费用需40元,每件乙产品的检验和销售费用需50元。Ⅰ车间每月可利用的工时为150小时,每小时的费用为80元;Ⅱ车间每月可利用的工时为200小时,每小时的费用为20元,估计下一年度平均每月可销售甲产品100台、乙产品80台。该公司根据这些实际情况制订月度计划的目标如下:

P1:检验和销售费用每月不超过6 000元;

P2:每月售出甲产品不少于100件;

P3:Ⅰ,Ⅱ两车间的生产工时应该得到充分利用;

P4:Ⅰ车间加班时间不超过30小时;

P5:每月乙产品的销售不少于80件。

问为完成上述目标,该公司应如何制订月度生产计划?

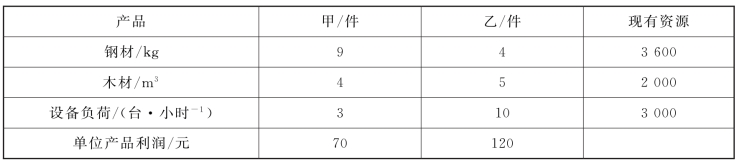
5-2 某工厂在计划期内要生产甲、乙两种产品,现有的资源及两种产品的技术消耗定额、单位利润如表5-17所示,试确定计划期内的生产计划,使利润最大,同时厂领导为适应市场需求,尽可能扩大甲产品的生产,甲的产量越大越好,权重分别为10和2,减少乙产品的生产,若提出目标P1(利润)的期望值e1＝45 000元,P2(甲产量)的期望值e2＝250件,P3(乙产量)的期望值e3＝200件,试建立该问题的数学模型。

表5-17

5-3 某制药公司有甲、乙两个工厂,现要生产A,B两种药品,均需在两个工厂生产。A 药品在甲厂加工2 h,然后送到乙厂检测包装2．5 h才能成品,B药品在甲厂加工4 h,再到乙厂检测包装1．5 h才能成品。A,B药品在公司内每月储存费分别为8元和15元。甲厂有12台制造机器,每台每天工作8 h,每月正常工作25天,乙厂有7台检测包装机,每天每台工作16 h,每月正常工作25天,每台机器每小时运行成本:甲厂为18元,乙厂为15元,单位产品A销售利润为20元,B为23元,根据市场预测,次月A,B两种药品的销售量估计分别为1 500单位和1 000单位。

该公司以下列次序为目标的优先次序,以实现次月的生产与销售目标:

P1:厂内的储存成本不超过23 000元。

P2:A药品的销售量必须完成1 500单位。

P3:甲、乙两个工厂的设备应全力运转,避免有空闲时间,把两个工厂的单位运转成本当作它们的权系数。

P4:甲厂超过作业时间全月不宜超过30 h。

P5:B药品的销量必须完成1 000单位。

P6:两个工厂的超时工作时间总和要求限制,其限制的比率以各厂每小时运转成本为准。

P7:利润不少于55 000元。

试确定A,B两种药品各生产多少,才能使目标达到最好?建立目标规划模型。

5-4 某公司生产A,B两种药品,这两种药品每小时的产量均为1 000盒,该公司每天采用两班制生产,每周最大工作时间为80小时,按预测,每周市场最大销量分别为70 000盒和45 000盒,A种药品每盒利润为2．5元,B种药品每盒利润为1．5元。试确定公司每周A,B两种药品的生产量x1和x2(单位:千盒),使公司的下列目标得以实现:

P1:避免每周80小时生产能力的过少使用;

P2:加班的时间限制在10小时以内;

P3:A,B两种药品的每周产量尽量分别达到70 000盒和45 000盒,但不得超出,其权系数以它们每盒的利润为准;

P4:尽量减少加班时间。

5-5 某医用器械厂生产甲、乙两种仪器,甲仪器每件可获利600元,乙每件可获利400元。生产每件甲、乙仪器所需机器台时数分别为2和3个单位,需劳动工时数分别为4和2个单位。假设厂方在计划期内可提供机器台时数100个单位,劳动工时数120个单位,如果劳动力不足,尚可组织工人加班,厂领导制定了下列目标:

P1:计划期内利润达到18 000元;

P2:机器台时数充分利用;

P3:尽量减少加班的工时数;

P4:甲产品产量达22件,乙产品产量达18件。(www.xing528.com)

请建立目标规划问题的数学模型,并用图解法求解。

5-6 某电台根据政策每天允许播出12小时,其中商业节目每分钟可收入250元,新闻节目每分钟支出40元,音乐节目每播一分钟支出17．5元。依政策规定,正常情况下商业节目只能占广播时间的20%,而每小时至少要安排5分钟的新闻节目。问该电台每天应如何安排节目?其优先级目标如下:

P1:满足政策的要求;

P2:每天的纯收入最大。

建立此问题的目标规划模型。

5-7 一个公司需要从两个仓库调拨同一种零部件给下属的三个工厂,每个仓库的供应能力、每个工厂的需求数量以及从每个仓库到每个工厂之间的单位运费如表5-18所示(表5-18中方格内的数字为单位运费)。

表5-18

公司提出的目标要求是:

P1:尽量满足工厂3的全部需求;

P2:其他两个工厂的需求至少分别满足75%;

P3:总运费要求最少;

P4:仓库2给工厂1的供应量至少为1 000单位;

P5:工厂1和工厂2的需求量满足程度尽可能平衡。

试建立该问题的目标规划模型。

5-8 有三个产地向四个销地供应物资,产地Ai(i＝1,2,3)的供应量ai、销地Bj(j＝1,2,3,4)的需要量bj、各产销地之间的单位物资cij如表5-19所示。ai和bj的单位为吨,cij的单位为元/吨。编制调运方案时需要依次考虑下列六个目标:

表5-19

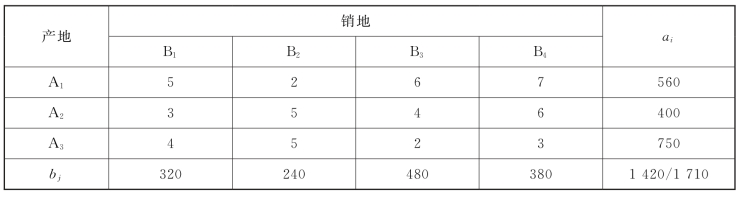
P1:B3是重点保证单位,其需要量应尽可能全部满足;

P2:A3向B3提供的物资不少于200吨;

P3:每个销地得到的物资数量不少于其需要量的80%;

P4:因路况原因,尽量避免安排A2的物资运往B1;

P5:对B2和B3的供应率要尽可能相同;

P6:实际的总运费不超过最小总运费(假设不考虑P1~P6各目标的最小运输费用S)。

试建立该问题的目标规划模型。

5-9 用图解法求解下列目标规划问题。

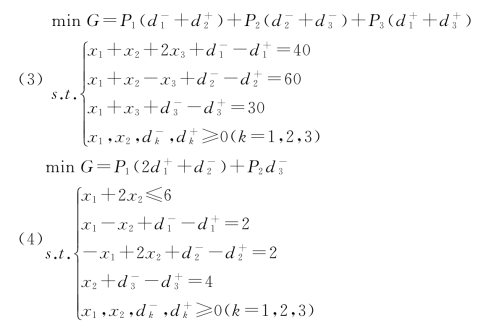
5-11 已知下面目标规则问题,分别用图解法和单纯形法求解。