使用单纯形法优化目标规划

下面举例说明目标规划单纯形法的求解步骤。

【例5-9】用单纯形法求解【例5-8】的目标规划问题。

视频-5．2．2目标规划单纯形法

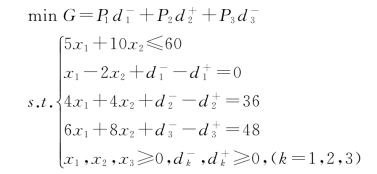
解:

标准化的模型为:

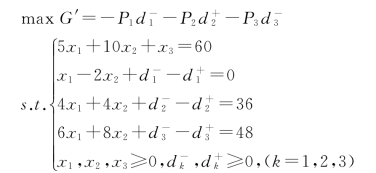
第一步,确定初始基(同线性规划单纯形法),计算检验数。

例如,σ1＝0－(0,－P1,0,－P3)(5,1,6,4)＝P1＋6P3,同理求出其他非基变量的检验数,如表5-6所示。

表5-6

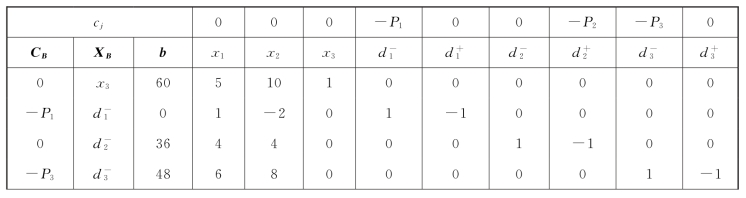
续表

第二步,最优性检验。目标规划的最优性检验是分优先级进行的,从P1级开始依次到Pk级为止,具体检验Pi级目标时,可能有下述三种情况:

①若检验数矩阵的Pi行系数均小于等于0,则Pi级目标已达最优,应转入对Pi＋1级目标的寻优,直到i＝k,计算结束。

②若检验数矩阵的Pj中有正系数,且正系数所在列的前i－1行优先因子的系数全为0,可判定该检验数为正,则选该系数(若此类正系数有多个,则可选绝对值最大者)所在列对应的非基变量为入基变量,继续进行基变换。如表5-6所示,确定初始基后,从检验数可确定出x1为入基变量,按最小比值法,则确定为出基变量,继续进行迭代变换。

③若检验数矩阵的Pi行中有正系数,但正系数所在列的前i－1行优先因子的系数为0,也有正数(没有负数),即整个检验数的值可判为正(因Pi－1≫Pi),故也应转入对Pi＋1级目标的寻优,否则会使高优先级别的目标函数值劣化。

第三步,基变换同线性规划的单纯形法,主元素的确定及迭代变换均同线性规划的单纯形法。

第四步,从表5-6中找到基本可行解和相应于各优先级的目标函数值。每个单纯形表中常数列b,即为各基变量的相应取值。本题最后一个单纯形表已为最优,它对应的满意解:其他变量为零,即X＝(24/5,12/5,12,0,0,36/5,0,0,0)T,与图解法得到的结果一致。以上求解过程如表5-7~表5-11所示。

表5-7

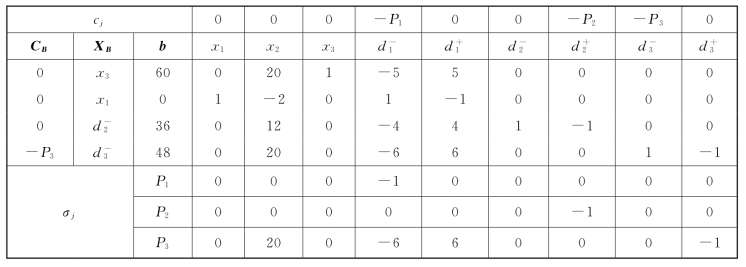
在最优单纯形表5-8中,非基变量的检验数都是零,故知本题有无穷多个满意解,如以为入基变量继续迭代,可得单纯形表5-9,对于已得到的满意解(x1＝8,x3＝20,,其他变量为零,即X＝(8,0,20,0,8,4,0,0,0)T。如以为入基变量继续迭代,可得单纯形表5-10,因此获得一个新的满意解其他变量为零,即X＝(6,3,0,0,0,0,0,0,12)T。再以单纯形表5-9中的作为入基变量,以作为出基变量继续迭代,还可以获得新的满意解其他变量为零,即X＝(9,0,15,0,9,0,0,0,6)T,如表5-11所示。以上四个满意解对应于图解法求解过程的四个顶点,如图5-14所示。

表5-8

表5-9

表5-10(www.xing528.com)

表5-11

【例5-10】用单纯形法求解下面目标规划问题。

解:

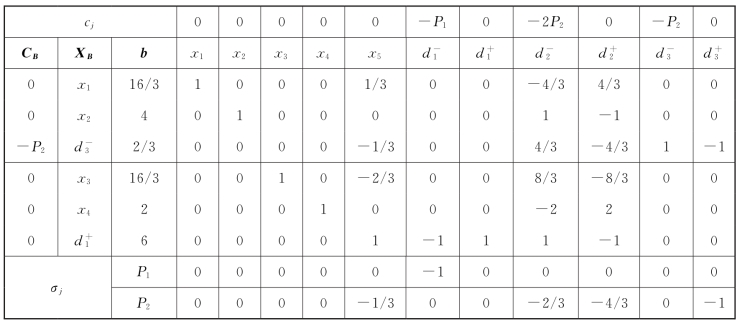
首先标准化,使用单纯形法求解,过程如表5-12和表5-13所示。

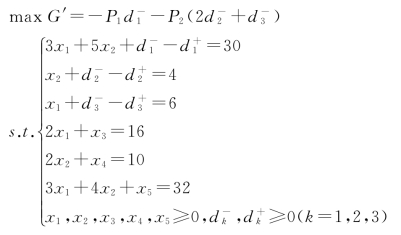
表5-12

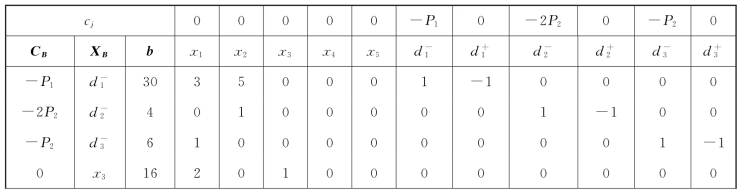
续表

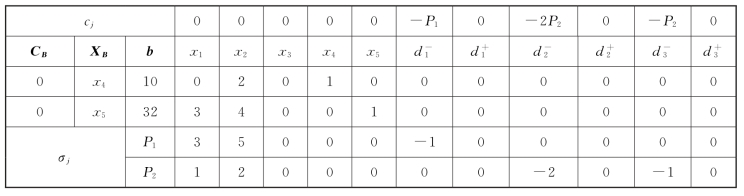
由表5-13可知即第二个目标中的第二个子目标没有满足。该问题具有唯一满意解:X＝(16/3,4,16/3,2,0,0,6,0,0,2/3,0)T。

表5-13

【例5-11】用单纯形法求解下面目标规划问题。

解:

先将模型标准化,求解过程如表5-14~表5-16所示。

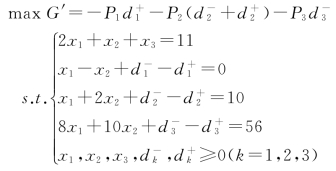
表5-14

表5-15

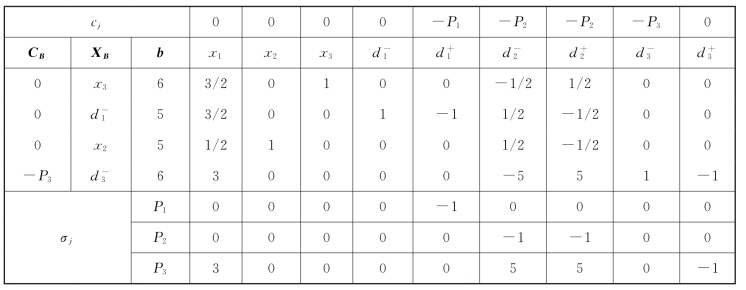
表5-16

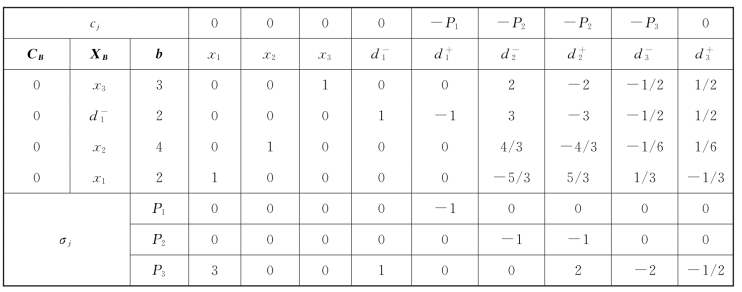
唯一满意解:X＝(2,4,3,2,0,0,0,0,0)T。