图解法：如何解决两个变量的目标规划问题？

视频-5．2．1目标规划图解法-1

视频-5．2．1目标规划图解法-2

视频-5．2．1目标规划图解法-3

视频-5．2．1目标规划图解法-4练习

对于两个变量的目标规划问题,可以用图解法求解,步骤如下:

第一步,按照系统(绝对)约束画出可行域;

第二步,先不考虑正负偏差变量,画出目标约束对应的边界线,然后在边界线上标出正负偏差变量;

第三步,按优先级和权重依次分析各级目标,寻找满意解。

【例5-6】用图解法求解【例5-3】中的目标规划问题。

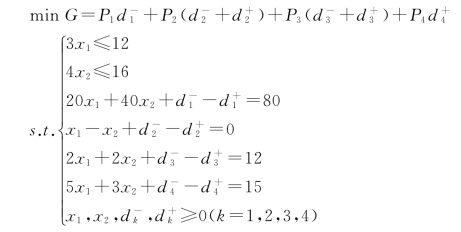
解:

第一步,确定可行域,如图5-1所示。

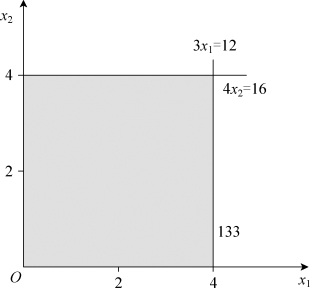
图5-1

第二步,画出目标约束对应的边界线,并标出正负偏差变量的方向,如图5-2所示。

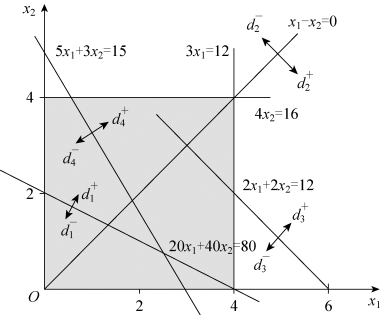
图5-2

第三步,确定满意解。满足目标的区域为一个多边形,如图5-3中的阴影部分。满足目标的区域为一条线段AB,如图5-4所示。满足目标的区域如图5-5所示,该问题在C点处获得满意解。

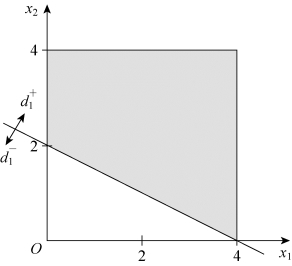
图5-3

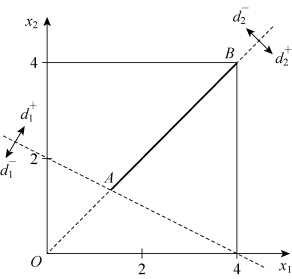
图5-4

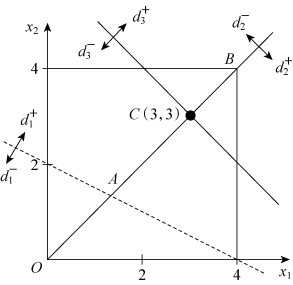
图5-5

从求解过程可知,该问题获得唯一满意解,因为只满足题中前三个目标P1,P2和P3,第四个目标没有达成。同时将x1＝3和x2＝3代入模型各约束条件中,可求出该满意解为:

X＝(3,3,3,4,0,100,0,0,0,0,0,9)T

其中,变量应按出场顺序排列,如X＝(x1,x2,x3,为松弛变量。需要注意的是,考虑低级别目标时,不能破坏已经满足的高级别目标。在有些目标规划中,当某一优先级的目标不能满足时,其后的某些低级别目标仍可能被满足。

【例5-7】用图解法求解下面目标规划问题。

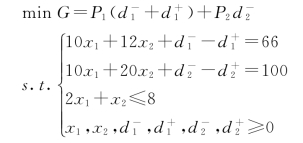
解:(www.xing528.com)

第一步,确定可行域,如图5-6所示。

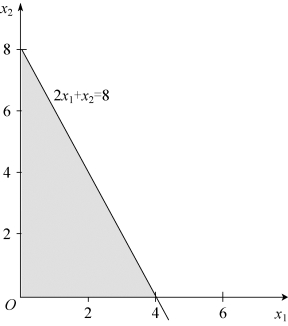
图5-6

第二步,画出目标约束对应的边界线,并标出正负偏差变量的方向,如图5-7所示。

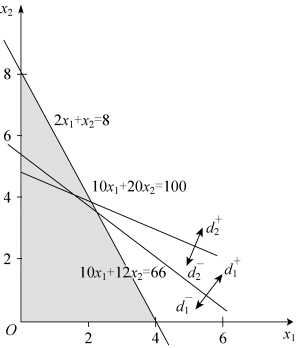
图5-7

第三步,寻找满意解。满足目标的区域为线段AB,如图5-8所示。满足目标的区域为一条线段AC,如图5-9所示,所以线段AC上任意一点都对应于满意解。可见,该目标规划问题具有无穷多满意解,其中,对应于A,C两个点的两个满意解为:

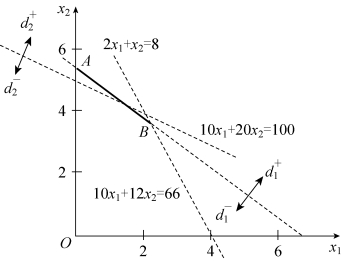
图5-8

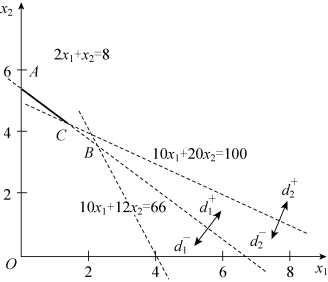
图5-9

X(1)＝(0,5．5,2．5,0,0,0,10)T

X(2)＝(1．5,4．25,0．75,0,0,0,0)T

【例5-8】用图解法求解下面目标规划问题。

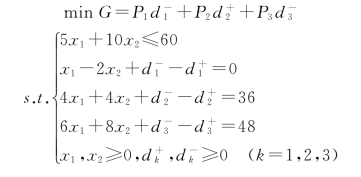
解:

第一步,确定可行域,如图5-10所示。

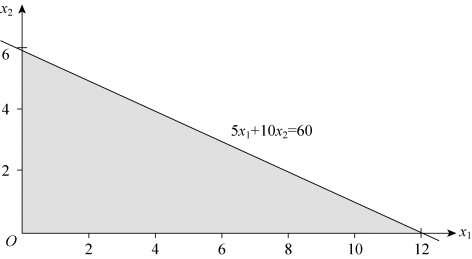
图5-10

第二步,画出目标约束对应的边界线,并标出正负偏差变量的方向,如图5-11所示。

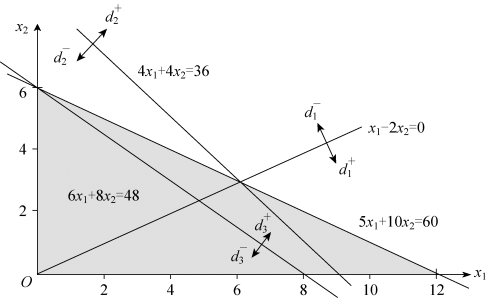
图5-11

第三步,确定满意解。满足目标的区域如图5-12所示,满足目标的区域如图5-13所示,满足目标的区域如图5-14所示,所以多边形ABCD上任意一点都对应于满意解。

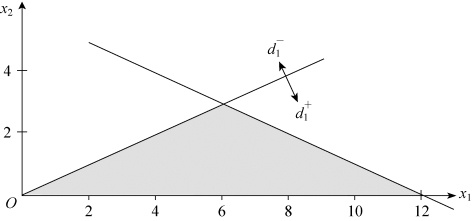
图5-12

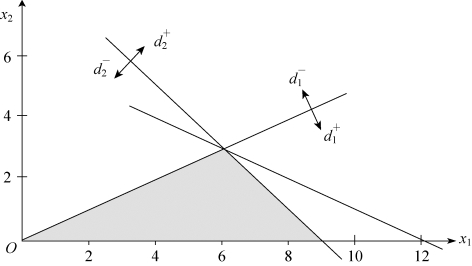
图5-13

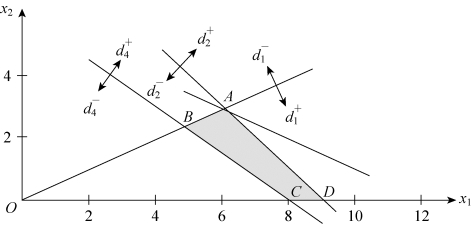
图5-14

所以该目标规划问题具有无穷多满意解,其中,对应于A,B,C,D四个点的满意解分别为:

X(1)＝(6,3,0,0,0,0,0,0,12)T

X(2)＝(4．8,2．4,12,0,0,7．2,0,0,0)T

X(3)＝(8,0,20,0,8,4,0,0,0)T

X(4)＝(9,0,15,0,9,0,0,0,6)T