
视频-5.1.3举例-1

视频-5.1.3举例-2

视频-5.1.3举例-3
【例5-3】某企业计划生产A,B两种产品,这些产品需要使用两种材料,要在两种不同设备上加工,相关资料如表5-3所示。
表5-3

问:在材料不能超用的条件下,企业如何安排生产计划?要求尽可能满足下列目标:
①力求使利润指标不低于80元;
②考虑到市场需求,两种产品的产量需相等(或保持1∶1的比例);
③设备A既要求充分利用(即设备A使用时间等于12),又尽可能不加班;
④设备B必要时可以加班,但加班时间尽可能少。
解:
设A,B两种产品的产量分别为x1,x2件,建模过程如下:
系统约束(硬约束):3x1≤12;4x2≤16。
目标约束(软约束):
P1:由于“力求使利润指标不低于80元”,即希望![]() 目标函数中应出现
目标函数中应出现![]() 则有
则有![]()
P2:由于“两种产品的产量相等”,即希望![]() 且权系数相等,则有
且权系数相等,则有![]()
P3:由于“设备A使用时间等于12”,即希望![]() 目标函数应出现
目标函数应出现![]() 且权系数相等,则有
且权系数相等,则有![]()
P4:由于“设备B必要时可以加班,但加班时间尽可能少”,说明![]() 可以大于零,同时又要求
可以大于零,同时又要求![]() 越小越好。如果目标函数中出现
越小越好。如果目标函数中出现![]() 则只能满足“
则只能满足“![]() 可以大于零”,但是
可以大于零”,但是![]() 的取值不受任何限制,不能满足“加班时间尽可能少”的要求,在这种情况下,目标函数只能出现
的取值不受任何限制,不能满足“加班时间尽可能少”的要求,在这种情况下,目标函数只能出现![]() ,因此有
,因此有![]()
综上:该目标规划问题的模型为:

【例5-4】某计算机公司计划这个月生产A,B,C三种型号的电脑。这三种型号的电脑需要在复杂的装配线上生产,生产1台A,B,C三种型号的电脑分别需要5 h、8 h和12 h。公司装配线正常的生产时间是每月1 700 h。公司营业部门估计A,B,C三种型号的电脑的利润分别是每台1 000元、1 440元、2 520元,而且,公司预测这个月生产的电脑能够全部售出。公司经理需要考虑以下目标:
P1:充分利用正常的生产能力,避免开工不足;
P2:优先满足老客户的需求:A,B,C三种型号的电脑50台、50台和80台,同时根据三种型号的电脑的单位时间利润分配不同的权系数;
P3:限制装配线加班时间,最好不要超过200 h;
P4:满足三种型号电脑的销售目标:A,B,C三种型号的电脑分别为100台、120台和100台,再根据三种型号电脑的单位时间利润分配不同的权系数;
P5:装配线的加班时间尽可能少。(https://www.xing528.com)
请建立目标规划问题的数学模型。
解:
根据已知条件,画出表5-4供建模时参考,并设A,B,C三种型号的电脑产量分别为x1,x2,x3台,分析过程如下:

表5-4

同理,对于其他目标:

综上,该目标规划问题的模型为:

思考:该模型目标函数中的权系数还可以如何表达?
【例5-5】有三个产地向四个销地供应物资。产地Ai(i=1,2,3)的供应量ai、销地Bj(j=1,2,3,4)的需要量bj、各产销地之间的单位物资cij如表5-5所示。ai和bj的单位为吨,cij的单位为元/吨。编制调运方案时需要依次考虑下列六个目标:
表5-5

P1:B4是重点保证单位,其需要量应尽可能全部满足;
P2:A3向B1提供的物资不少于100吨;
P3:每个销地得到的物资数量不少于其需要量的80%;
P4:实际的总运费不超过最小总运费的110%(不考虑P1至P6各目标);
P5:因路况原因,尽量避免安排A2的物资运往B4;
P6:对B1和B3的供应率要尽可能相同。
试建立该问题的目标规划模型。
解:
设第i个产地向第j个销地的物资调运量为xij(i=1,2,3;j=1,2,3,4),在不考虑P1至P6各目标时求解运输问题,得知最优方案不唯一,其中一个方案为:

建模过程如下:

同时考虑系统约束,得到该问题的目标规划模型为:

综上,对于n个决策变量、m个系统约束、k个目标、i个优先等级的目标规划问题,模型一般包括以下要素:
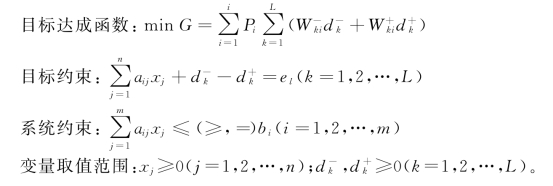
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




