某公司未来三年投资工程及费用分析

4-1 高压容器公司制造小、中、大三种尺寸的金属容器,所用资源为金属板、劳动力和机器设备,制造一个容器所需的各种资源的数量如表4-16所示。不考虑固定费用,每种容器售出一只所得的利润分别为4万元、5万元、6万元,可使用的金属板有500吨,劳动力有300人/月,机器有100台/月,此外,不管每种容器制造的数量是多少,都要支付一笔固定的费用,小号是100万元,中号为150万元,大号为200万元。试制定一个生产计划,使获得的利润为最大,并建立相关数学模型。

表4-16

4-2 某产品有A1和A2两种型号,需经过B1,B2,B3三道工序,单位工时、利润、各工序每周工时限制如表4-17所示,问工厂如何安排生产,才能使总利润最大?(B3工序有两种加工方式B31和B32,只能选择其中一种;产品单位为件)

表4-17

4-3 某厂可生产四种产品,对于三种主要资源的单位消耗及单位利润如表4-18所示,如果生产产品3需要用一种特殊的机器,这种机器的固定成本(启用成本)为3 000元,生产产品2和产品4同样需要共用一种特殊的机器加工,其固定成本(启用成本)为1 000元,写出求利润最大的线性规划模型。

表4-18

4-4 某公司今后三年内有五项工程可以考虑投资,每项工程的预期收入和年度费用如表4-19所示。

表4-19

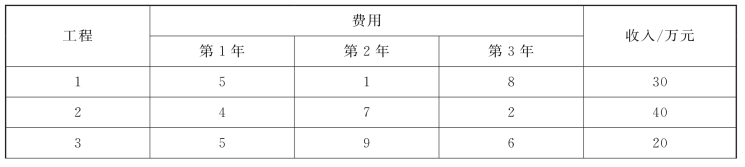
续表

每项工程都需要三年完成,问应选择哪些项目,才能使总收入最大?试建立该问题的数学模型。

4-5 某部门一周中每天需要不同数目的雇员,周一到周四每天至少需要50人,周五至少需要80人,周六、周日每天至少需要90人,现规定应聘者需要连续工作5天,试确定聘用方案,即周一到周日每天聘用多少人,使得在满足需要的条件下,聘用总人数最少?请建立相关的数学模型。

4-6 一辆货车的有效载重量是20吨,载货有效空间是8 m×2 m×1．5 m。现有六件货物可供选择运输,每件货物的重量、体积及收入如表4-20所示。另外,在货物4和5中优先运货物5,货物1和货物2不能混装,货物3和货物6要么都不装,要么同时装。问怎样安排货物运输方案,才能使收入最大?并建立相关的数学模型。

表4-20

4-7 京成畜产品公司计划在市区的东、西、南、北四区建立销售门市部,有10个位置Aj(j＝1,2,…,10)可供选择,考虑到各地区居民的消费水平及居民居住密集度,规定在东区从A1,A2,A3三个点中至多选两个,在西区从A4,A5两个点中至少选一个,在南区从A6,A7两个点中至少选一个,在北区从A8,A9,A10三个点中至少选两个。Aj各点的设备投资及每年可获利润由于地点不同都是不一样的,预测情况如表4-21(单位:万元)所示。但投资总额不能超过720万元,问应选择哪几个销售点,可使每年获得的利润最大?请建立相关的数学模型。

表4-21

4-8 以汉江、长江为界将武汉市划分为汉口、汉阳和武昌三镇。某商业银行计划投资9 000万元在武汉市备选的12个点考虑设立支行,如图4-14所示。每个点的投资额与一年的收益如表4-22所示。计划汉口投资设立2~3个支行,汉阳投资设立1~2个支行,武昌投资设立3~4个支行。问如何投资,可使总收益最大?试建立该问题的数学模型,并回答是什么模型?可以用什么方法求解?

图4-14

表4-22

4-9 女子体操团体赛规定:

①每个代表队由5名运动员组成,比赛项目是高低杠、平衡木、鞍马及自由体操。

②每个运动员最多只能参加3个项目并且每个项目只能参赛一次;(www.xing528.com)

③每个项目至少要有人参赛一次,并且总的参赛人次数等于10;

④每个项目采用10分制记分,将10次比赛的得分求和,按其得分高低排名,分数越高,成绩越好。

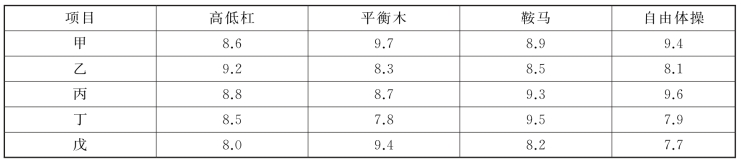
已知代表队5名运动员各单项的预赛成绩如表4-23所示。问怎样安排运动员的参赛项目,使团体总分最高?试建立该问题的数学模型。

表4-23

4-10 甲、乙、丙、丁四人加工A,B,C,D四种工件所需时间(分钟)如表4-24所示,问应指派何人加工何种工件,才能使总的加工时间最少?要求建立数学模型并求解。

表4-24

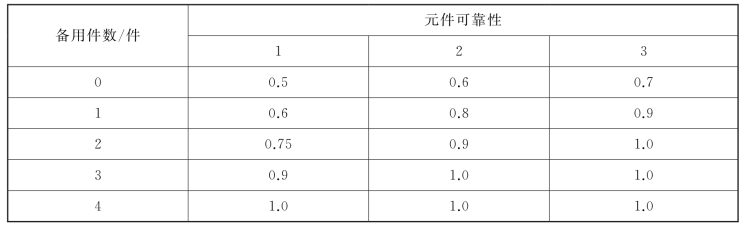
4-11 某电子系统由3种元件组成,为了使系统正常运转,每个元件都必须工作良好,如一个或多个元件安装几个备用件将提高系统的可靠性,已知系统运转可靠性为各元件可靠性的乘积,而每个元件的可靠性是备用件数量的函数,具体如表4-25所示。3种元件的价格分别为30元/件、40元/件和50元/件,重量分别为2 kg/件、4 kg/件和6 kg/件。而全部备用件的费用预算限制为220元,重量限制为20 kg,问每种元件各安装多少个备用件,可使系统可靠性最大?试建立该问题的整数(非线性)规划数学模型。

表4-25

4-12 用分枝定界法求解下列整数规划问题。

4-15 用匈牙利法求解下列指派问题。

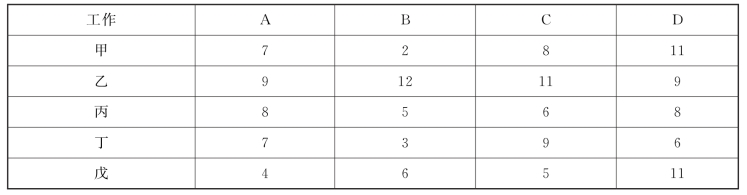
4-16 有五个工人甲、乙、丙、丁、戊,要指派他们完成四项工作A,B,C,D,每项工作只能由1个工人承担,每人做各项工作所耗的成本如表4-26所示。问如何指派,才能使成本最小。

表4-26

4-17 现有四个人、五项工作,每人做每项工作所耗时间如表4-27所示,问如何指派,才能使总时间最短?

表4-27

4-18 由建筑公司A1,A2,A3来承建B1,B2,B3,B4,B5五项工程,相关资料如表4-28所示,现允许每家建筑公司承建一项或两项工程,求使总费用最少的指派方案。

表4-28

4-19 分配甲、乙、丙、丁四个人去完成A,B,C,D,E五项任务,每人完成各项任务的时间如表4-29所示。由于任务重,人数少,需要考虑以下要求:

表4-29

①任务E必须完成,其他四项任务可选三项完成,但甲不能做A项任务;

②其中有一人完成两项任务,其他人每人完成一项任务。

试确定最优指派方案,使完成任务的总时间最少。