如何使用匈牙利法解决指派问题

视频-4．2．5整数规划求解-5-匈牙利法

1955年,库恩(W．W．Kuhn)根据匈牙利数学家康尼格(D．Koumlnig)得出的结论,提出了求解指派问题的方法——匈牙利法(Hungarian Method),即康尼格定理,用于求解目标函数最小化的指派问题。其理论依据是若指派问题的系数矩阵C＝(cij)n×n的某行(或某列)各元素分别加上一个常数k(可以为正数,也可以为负数),得到一个新的矩阵C′＝(c′ij)n×n,则这两个矩阵所对应的指派问题的最优解相同。在求解时遵循康尼格定理:矩阵中独立零元素的最多个数等于能覆盖所有零元素的最少直线数。根据这个定理,对于n阶效率矩阵,匈牙利法求解指派问题的步骤如下:

(1)首先让效率矩阵中的每行(列)都出现零元素。

若效率矩阵某行(列)中没有零元素,则该行(列)所有元素都减去该行(列)中的最小元素。

(2)寻找独立零元素。

独立零元素有狭义和广义之分。狭义的独立零元素,是指若某行(列)中只有一个零,那么这个零就是独立零元素,而且各个独立零元素应分别位于不同的行或列中,即每行(列)中只有一个独立零元素。当独立零元素的数量等于n时,计算停止,此时将效率矩阵中独立零元素变为“1”,其他元素变为“0”,则获得最优解。若独立零元素的数量小于n,则重复第(3)步,直至找到n个独立零元素为止。

(3)继续寻找独立零元素。

若独立零元素的数量小于n,说明在进行第(2)步时,同列(行)不同行(列)都出现了独立零元素,此时只能选择某一行(列)的“0”作为独立零元素,因而放弃选择其他行(列)的独立零元素,因此,应以这两行(列)为对象做进一步的处理。将这两行(列)中的元素都减去除“0”以外的最小元素,同时对出现负元素的列(行)中的元素都加上一个元素(即负值中绝对值最大的相反数),目的是使该列(行)中的元素均为非负且出现零元素。重复步骤(2)和步骤(3),直到独立零元素的数量等于n。

需要说明的是,在继续寻找独立零元素的过程中,独立零元素可能从狭义变为广义,下面举例说明匈牙利法的求解过程。

【例4-15】已知某指派问题的效率矩阵如公式(4-11)所示,请用匈牙利法求解。

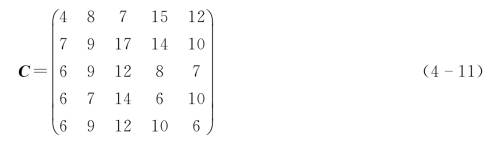
解:

第一步,每行元素都减去该行中最小元素“4”,“7”,“6”,“6”和“6”,则矩阵C转化为公式(4-12)。

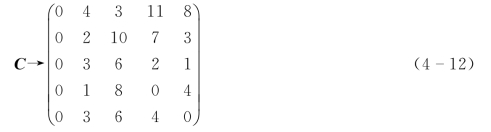
第二步,对于公式(4-12),第2、第3列元素都减去该列中最小元素“1”和“3”,则矩阵C转化为公式(4-13)。

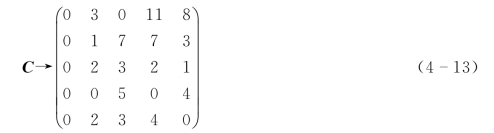
第三步,寻找独立零元素。对于公式(4-13),选择狭义独立零元素,见公式(4-14)。

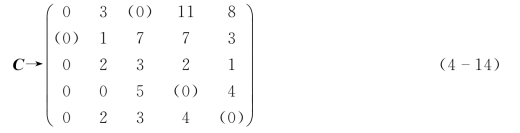
在公式(4-14)中,第2行和第3行的第1列(或第2列和第4列的第4行)均存在狭义独立零元素,不妨选择第2行中的独立零元素。由于独立零元素的数量“4”小于效率矩阵C的阶数“5”,因此需要继续寻找独立零元素。

第四步,将第2行和第3行的所有元素分别减去除“0”以外的最小元素“1”,得到公式(4-15)。

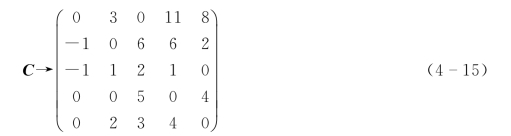
第五步,将公式(4-15)中第1列所有元素都加上“1”{max[－(－1),－(－1)]},得到公式(4-16)。

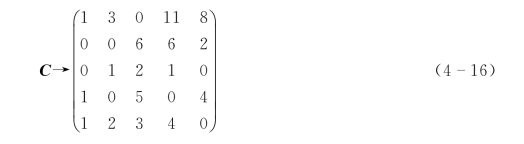
第六步,对于公式(4-16),寻找独立零元素,见公式(4-17)。

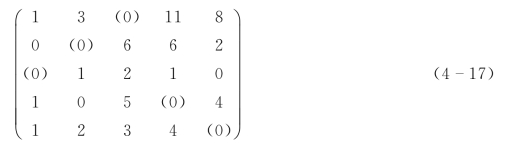
第七步,将公式(4-17)中的独立零元素均变为“1”,其他元素变为“0”,得到该指派问题的最优解,见公式(4-18)。(www.xing528.com)

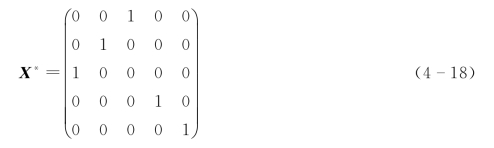
综上,该指派问题的最优方案为第1个人完成第3项任务,第2个人完成第2项任务,第3个人完成第1项任务,第4个人完成第4项任务,第5个人完成第5项任务,花费的成本(或时间)为34(7＋9＋6＋6＋6)。

对于求最大值、人数和任务数不相等以及不可接受的配置(如某个人不能完成某项任务)等特殊指派问题,要对效率矩阵通过适当变换后使用匈牙利法求解。

(1)求最大化的指派问题。

如果指派问题求最大值,用M(效率矩阵中的最大元素)减去效率矩阵C中所有元素得到矩阵B＝(bij),bij＝M－cij,求矩阵B的最小值,矩阵B与矩阵C的最优解相同。

【例4-16】人事部门打算安排甲、乙、丙、丁4个人到A,B,C,D 4个不同的岗位工作,每个岗位一个人。经考核,4个人在不同岗位的成绩如表4-14所示,问如何安排他们的工作,才使得总成绩最好?

表4-14

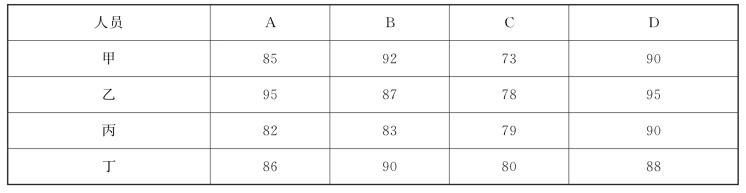
解:

令M＝max{cij}＝95,bij＝95－cij≥0,则有:

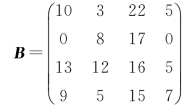
求解结果为:

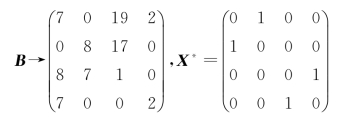
综上,Z∗＝92＋95＋90＋80＝357,最优指派方案为甲完成任务B,乙完成任务A,丙完成任务D,丁完成任务C,最高成绩为357。

(2)人数和任务数不相等的指派问题。

这类问题的处理方式类似产销不平衡的运输问题。假设指派问题人数为m,任务数为n。当m≠n时,将指派问题转化成m＝n的问题,再用匈牙利法求解。一般来说,当m＞n时,虚拟m－n项工作,对应的效率为零;当m＜n时,虚拟n－m个人,对应的效率为零;当某个人不能完成某项任务时,对应的效率为M。

【例4-17】某商业集团计划在市内4个点投资4个专业超市,考虑的商品有电器、服装、食品、家具及计算机5个类别。通过评估,家具超市不能放在第3个点,计算机超市不能放在第4个点,不同类别的商品投资到各点的年利润(万元)预测值如表4-15所示。问该商业集团如何做出投资决策,才能使年利润最大?

表4-15

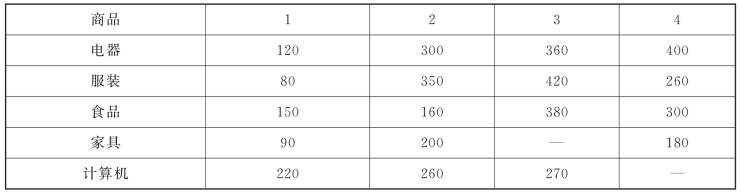
解:

根据题意,c43＝c54＝0,则效率矩阵为:

令M＝420,将该指派最大化问题转化为最小化问题,同时虚拟一个地点5,则效率矩阵转化为:

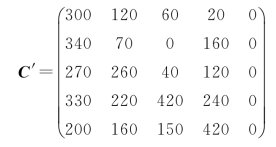
用匈牙利法求解过程和结果如下: