隐枚举法：加速0-1整数规划问题的求解

视频-4．2．4整数规划问题求解-4-隐枚举法

在线性规划问题的模型中,当变量的取值只能是“0”或“1”时,称之为“0—1整数规划问题”(或0—1规划问题)。对于0—1整数规划问题,有一种极其简单的解法,就是将变量取值为0或1的所有组合列出,然后分别代入目标函数,选出其中能使目标函数最优化的组合,即为最优解。如果变量较少(如不超过3个),是不难枚举的,但是当变量较多时,可能解将呈指数剧增,如果靠经验枚举求解,难以做到快捷有效。

为解决0—1规划的求解问题,Balas E在1965年提出了隐枚举法,目前隐枚举法(Implicit Enumeration Algorithm)已经成为求解“0—1整数规划问题”的常见方法,其基本思想是通过增加过滤约束舍弃一定不是最优解的解组合(简称组合)以求得最优解。“隐”的含义是指在检验可能解的可行性和非劣性过程中,增加一个过滤条件,以加快筛选过程,其应用前提是要枚举出所有可能解的集合。对具有n个变量的0—1整数规划问题来说,可能解的个数为2n。下面举例说明隐枚举法的求解步骤。

(1)目标函数求“max”的0—1整数规划问题。

【例4-13】求下面0—1整数规划问题的最优解。

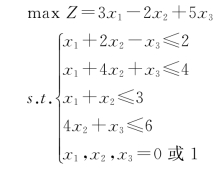
解:

①寻找目标函数值下界。可以判断,当可行解X＝(0,1,0)T时,该问题的目标函数值(－2)最小,因此可以确定目标函数值下界,即3x1－2x2＋5x3≥－2。

②构造过滤约束,并将其加入原约束条件中。

因目标函数值大于等于－2,因此可能是0[X＝(0,0,0)T],3[X＝(1,0,0)T]和5[X＝(0,0,1)T]等,可先构造过滤约束“3x1－2x2＋5x3≥3”,则原模型变为:

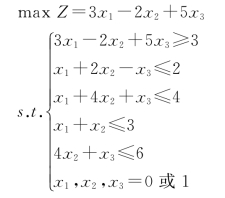
③写出所有解组合,比较目标函数值Z,并检查是否满足约束条件和过滤条件,得出最优解。过滤约束“3x1－2x2＋5x3≥3”的求解过程如表4-11所示。

在表4-11中,从上往下看,Z值为零,小于过滤约束对应的目标值,因此隐去。当X＝(0,0,1)T时,满足所有约束条件(包括过滤约束),因此在表4-11中对应位置填入“√”,此时目标函数值Z为“5”。接下来,目标函数值为“－2”“3”“3”,均小于5,因此隐去。当X＝(1,0,1)T时,满足所有约束条件,因此在表4-11中对应位置添入“√”,此时目标函数值Z为“8”。接下来,目标函数值均小于8,所以隐去,于是该问题的最优解为:X∗＝(1,0,1)T,Z∗＝8。

表4-11

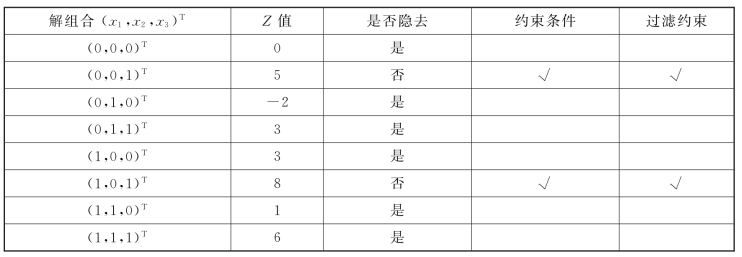
可见,添加过滤约束可以加快筛选过程,隐去不可能成为最优解的解组合,以简化求解过程。但需注意,过滤约束一定要满足原约束条件。同时,为保证解组合不遗漏,可参照二进制的表达方法,将所有解依次列出,本题因有三个变量,故解组合的数量为23＝8。(www.xing528.com)

也可构造过滤约束“3x1－2x2＋5x3≥5”[X＝(0,0,1)T],也可以按表4-11中从下到上的顺序寻找最优解,求解过程如表4-12所示。

表4-12

续表

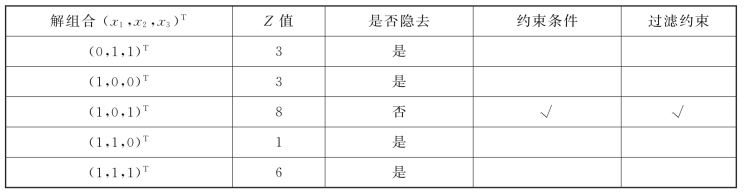
当然,对于本题如果构造过滤约束“3x1－2x2＋5x3≥8”[X＝(1,0,1)T],求解过程将更加快捷。因此,在目标函数求最大值的“0—1整数规划问题”时,为使求解过程更加简捷,应在多个过滤约束中选取右端常数较大的过滤约束,过滤约束右端项越大,求解越快捷。

(2)目标函数求“min”的0—1整数规划问题。

对于目标函数求最小值的“0—1整数规划问题”,求解步骤与求最大值时有所区别,应首先寻找目标函数值上界,其他步骤则与求最大值相同。主要技巧是在可能构造的多个过滤约束中选取右端常数较小的过滤约束,过滤约束右端项越小,求解越快捷。

【例4-14】求以下0—1整数规划问题的最优解。

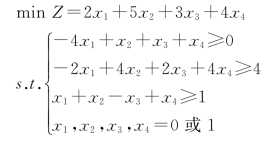
解:

对于本题(解组合数量为24＝16),可构造过滤约束“2x1＋5x2＋3x3＋4x4≤4”[X＝(0,0,0,1)T],求解过程(从上到下顺序)如表4-13所示,结果为X∗＝(0,0,0,1)T,Z∗＝4。

表4-13

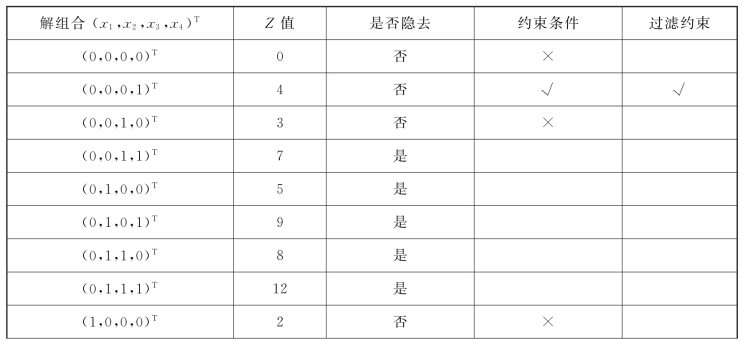
续表